And/or Trees

AND/OR Trees: We will next show the use of AND/OR trees for inferencing in Horn clause systems. The problem is, given a set of axioms in Horn clause form and a goal, show that the goal can be proven from the axioms.

An AND/OR tree is a tree whose internal nodes are labeled either "AND" or "OR". A valuation of an AND/OR tree is an assignment of "TRUE" or "FALSE" to each of the leaves. Given a tree T and a valuation over the leaves of T, the values of the internal nodes and of T are defined recursively in the obvious way:

• An OR node is TRUE if at least one of its children is TRUE.
• An AND node is TRUE if all of its children are TRUE.

The above is an unconstrained AND/OR tree. Also common are constrained AND/OR trees, in which the leaves labeled "TRUE" must satisfy some kind of constraint. A solution to a constrained AND/OR tree is a valuation that satisfies the constraint and gives the tree the value "TRUE".

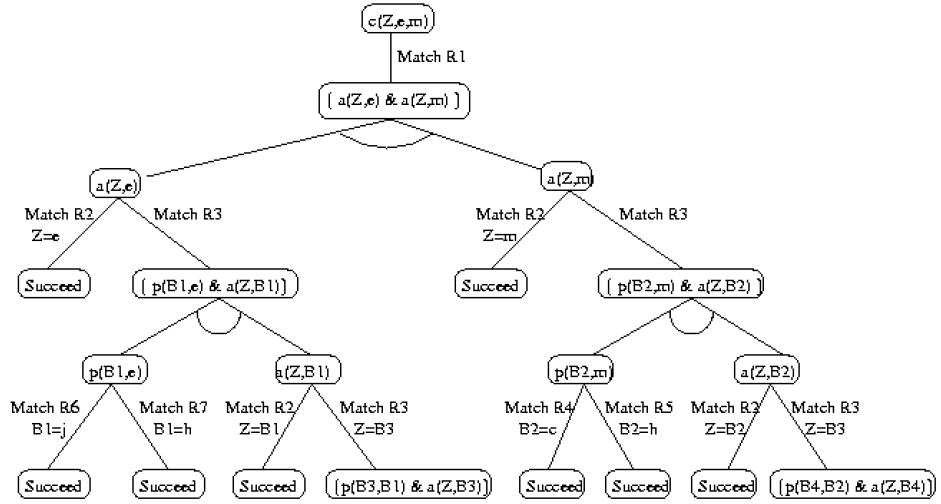
An OR node is a goal to be proven. A goal G has one downward arc for each rule R whose head resolves with G. This leads to an AND node. The children in the AND node are the literals in the tail of R. Thus, a rule is satisfied if all its subgoals are satisfied (the AND node); a goal is satisfied if it is established by one of its rules (the OR node). The leaves are unit clauses, with no tail, labeled TRUE, and subgoals with no matching rules, labeled FALSE . The constraint is that the variable bindings must be consistent. The figure below show the AND/OR tree corresponding to the following Prolog rule set with the goal "common_ancestor(Z,edward,mary)"

Axioms:
/* Z is a common ancestor of X and Y */
R1: common_ancestor(Z,X,Y) :- ancestor(Z,X), ancestor(Z,Y).
/* Usual recursive definition of ancestor, going upward. */
R2: ancestor(A,A).
R3: ancestor(A,C) :- parent(B,C), ancestor(A,B).
/* Mini family tree */
R4: parent(catherine,mary).
R5: parent(henry,mary).
R6: parent(jane,edward).
R7: parent(henry,edward).