Bi-directional Search

Bi-directional search: Suppose that the search problem is such that the arcs are bidirectional. That is, if there is an operator that maps from state A to state B, there is another operator that maps from state B to state A. Many search problems have reversible arcs. 8-puzzle, 15-puzzle, path planning etc are examples of search problems. However there are other state space search formulations which do not have this property. The water jug problem is a problem that does not have this property. But if the arcs are reversible, you can see that instead of starting from the start state and searching for the goal, one may start from a goal state and try reaching the start state. If there is a single state that satisfies the goal property, the search problems are identical.
How do we search backwards from goal? One should be able to generate predecessor states. Predecessors of node n are all the nodes that have n as successor. This is the motivation to consider bidirectional search.

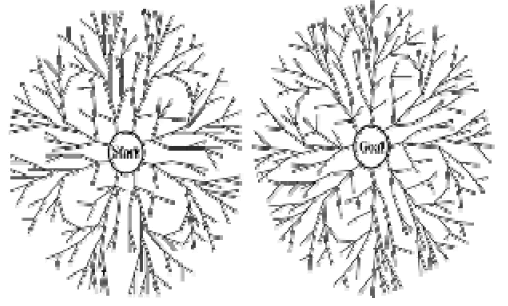
Algorithm: Bidirectional search involves alternate searching from the start state toward the goal and from the goal state toward the start. The algorithm stops when the frontiers intersect.

A search algorithm has to be selected for each half. How does the algorithm know when the frontiers of the search tree intersect? For bidirectional search to work well, there must be an efficient way to check whether a given node belongs to the other search tree.
Bidirectional search can sometimes lead to finding a solution more quickly. The reason can be seen from inspecting the following figure.

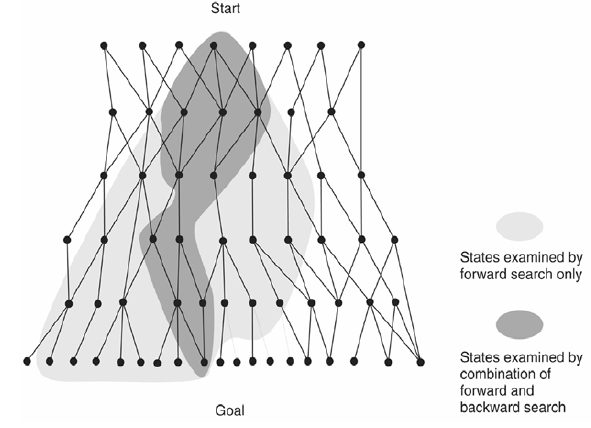
Also note that the algorithm works well only when there are unique start and goal states. Question: How can you make bidirectional search work if you have 2 possible goal states?
Time and Space Complexities: Consider a search space with branching factor b. Suppose that the goal is d steps away from the start state. Breadth first search will expand O(bd) nodes. If we carry out bidirectional search, the frontiers may meet when both the forward and the backward search trees have depth = d/2. Suppose we have a good hash function to check for nodes in the fringe. IN this case the time for bidirectional search will be O((bd/2). Also note that for at least one of the searches the frontier has to be stored. So the space complexity is also O((bd/2).

Comparing Search Strategies: