Concept Learning
Concept Learning: Definition: The problem is to learn a function mapping examples into two classes: positive and negative. We are given a database of examples already classified as positive or negative. Concept learning: the process of inducing a function mapping input examples into a Boolean output.
Examples:
- Classifying objects in astronomical images as stars or galaxies
- Classifying animals as vertebrates or invertebrates
Example: Classifying Mushrooms
- Class of Tasks: Predicting poisonous mushrooms
- Performance: Accuracy of classification
- Experience: Database describing mushrooms with their class
- Knowledge to learn: Function mapping mushrooms to {0,1} where 0:not-poisonous and 1:poisonous
- Representation of target knowledge: conjunction of attribute values.
- Learning mechanism: candidate-elimination
Representation of instances:
Features:
- color {red, brown, gray}
- size {small, large}
- shape {round,elongated}
- land {humid,dry}
- air humidity {low,high}
- texture {smooth, rough}
Input and Output Spaces:
- X : The space of all possible examples (input space).
- Y: The space of classes (output space).
An example in X is a feature vector X.
- For instance: X = (red,small,elongated,humid,low,rough)
- X is the cross product of all feature values.
Only a small subset of instances is available in the database of examples.
Training Examples:
D : The set of training examples.
D is a set of pairs { (x,c(x)) }, where c is the target concept. c is a subset of the universe of discourse or the set of all possible instances.
Example of D:
((red,small,round,humid,low,smooth), poisonous)
((red,small,elongated,humid,low,smooth), poisonous)
((gray,large,elongated,humid,low,rough), not-poisonous)
((red,small,elongated,humid,high,rough), poisonous)
Hypothesis Representation
Any hypothesis h is a function from X to Y
h: X -> Y
We will explore the space of conjunctions.
Special symbols:
- ? Any value is acceptable
- 0 no value is acceptable
Hypotheses Space:
The space of all hypotheses is represented by H
Let h be a hypothesis in H.
Let X be an example of a mushroom.
if h(X) = 1 then X is poisonous, otherwise X is not-poisonous
Our goal is to find the hypothesis, h*, that is very “close” to target concept c.
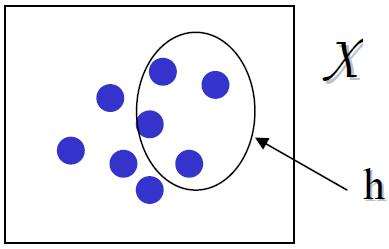
A hypothesis is said to “cover” those examples it classifies as positive.
Assumptions:
- We will explore the space of all conjunctions.
- We assume the target concept falls within this space.
- A hypothesis close to target concept c obtained after seeing many training examples will result in high accuracy on the set of unobserved examples. (Inductive Learning Hypothesis)