Concept Learning As Search

Concept Learning as Search: We will see how the problem of concept learning can be posed as a search problem. We will illustrate that there is a general to specific ordering inherent to any hypothesis space.

Consider these two hypotheses:
h1 = (red,?,?,humid,?,?)
h2 = (red,?,?,?,?,?)
We say h2 is more general than h1 because h2 classifies more instances than h1 and h1 is covered by h2.

For example, consider the following hypotheses

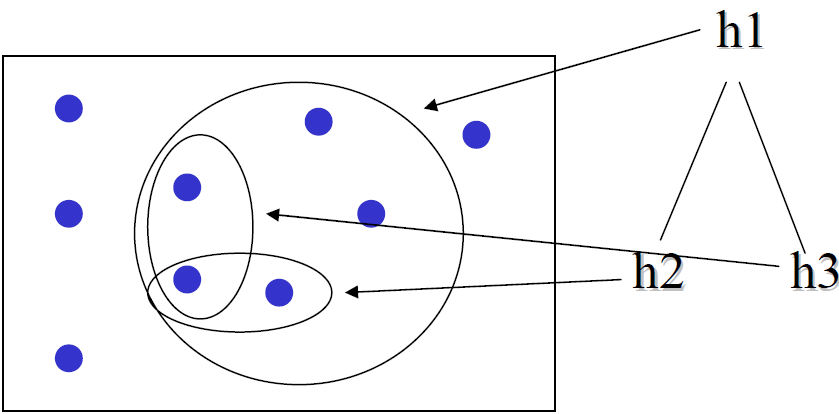
h1 is more general than h2 and h3.
h2 and h3 are neither more specific nor more general than each other.

Definitions: Let hj and hk be two hypotheses mapping examples into {0,1}.
We say hj is more general than hk iff
For all examples X, hk(X) = 1 -> hj(X) = 1
We represent this fact as hj >= hk
The >= relation imposes a partial ordering over the hypothesis space H (reflexive, antisymmetric, and transitive).

Any input space X defines then a lattice of hypotheses ordered according to the general-specific relation: