Extending Semantic Nets
Extending Semantic Nets: Here we will consider some extensions to Semantic nets that overcome a few problems or extend their expression of knowledge.
Partitioned Networks Partitioned Semantic Networks allow for:
- propositions to be made without commitment to truth.
- expressions to be quantified.
Basic idea: Break network into spaces which consist of groups of nodes and arcs and regard each space as a node.
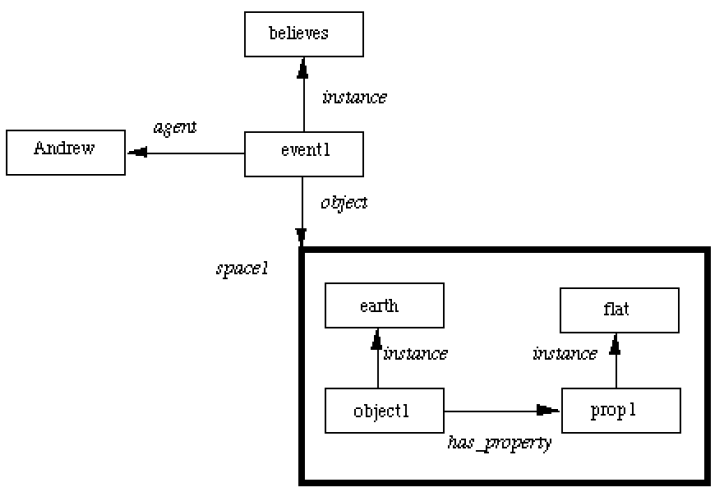
Consider the following: Andrew believes that the earth is flat. We can encode the proposition the earth is flat in a space and within it have nodes and arcs the represent the fact (next figure). We can the have nodes and arcs to link this space the the rest of the network to represent Andrew's belief.
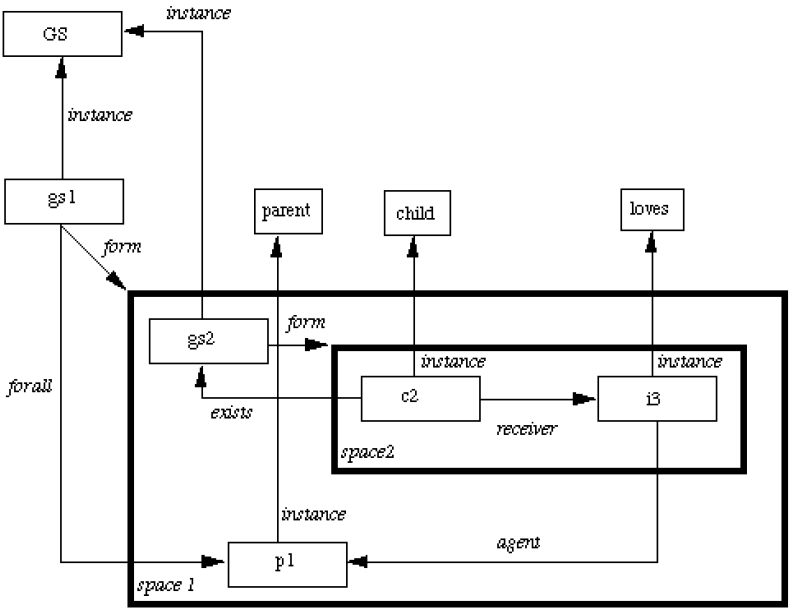
Now consider the quantified expression: Every parent loves their child To represent this we:
- Create a general statement, GS, special class.
- Make node g an instance of GS.
- Every element will have at least 2 attributes:
- a form that states which relation is being asserted.
- one or more forall
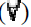() or exists 
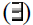() connections -- these represent universally quantifiable variables in such statements e.g. x, y in parent(x) 
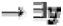: child(y) 
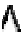loves(x,y)
Here we have to construct two spaces one for each x,y. NOTE: We can express variables as existentially qualified variables and express the event of love having an agent p and receiver b for every parent p which could simplify the network.
Also If we change the sentence to Every parent loves child then the node of the object being acted on (the child) lies outside the form of the general statement. Thus it is not viewed as an existentially qualified variable whose value may depend on the agent. So we could construct a partitioned network as in the next figure.
Version
