Hidden Markov Model

A hidden Markov model (HMM) an augmentation of the Markov chain to include observations. Just like the state transition of the Markov chain, an HMM also includes observations of the state. These observations can be partial that different states can map to the same observation and noisy that the same state can stochastically map to different observations at different times.

The assumptions behind an HMM are that the state at time t 1 only depends on the state at time t, as in the Markov chain. The observation at time t only depends on the state at time t. The observations are modeled using the variable O_t for each time t whose domain is the set of possible observations. The belief network representation of an HMM is depicted in Figure 6.14. Although the belief network is shown for four stages, it can proceed indefinitely.

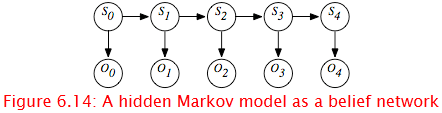
A stationary HMM includes the following probability distributions:

• P(S₀) specifies initial conditions.
• P(S_{t 1}|S_t) specifies the dynamics.
• P(O_t|S_t) specifies the sensor model.

There are a number of tasks that are common for HMMs.

The problem of filtering belief-state monitoring to determine the current state based on the current and previous observations, namely to determine

P(S_i|O₀,...,O_i).

Note that all state and observation variables after S_i are irrelevant because they are not observed and can be ignored when this conditional distribution is computed.

The problem of smoothing to determine a state based on past and future observations. Suppose an agent has observed up to time k and wants to determine the state at time i for i<k; the smoothing problem is to determine

P(S_i|O₀,...,O_k).

All of the variables S_i and V_i for i>k can be ignored.

Localization: Suppose a robot wants to determine its location based on its history of actions and it sensor readings. This is the problem of localization.

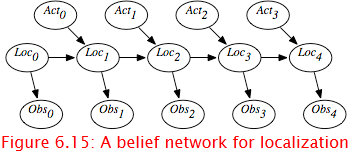
Figure 6.15 shows a belief-network representation of the localization problem. There is a variable Loc_i for each time i, which represents the robot's location at time i. There is a variable Obs_i for each time i, which represents the robot's observation made at time i. For each time i, there is a variable Act_i that represents the robot's action at time i. In this section, assume that the robot's actions are observed.

This model assumes the following dynamics: At time i, the robot is at location Loc_i, it observes Obs_i, then it acts, it observes its action Act_i, and time progresses to time i 1, where it is at location Loc_{i 1}. Its observation at time t only depends on the state at time t. The robot's location at time t 1 depends on its location at time t and its action at time t. Its location at time t 1 is conditionally independent of previous locations, previous observations, and previous actions, given its location at time t and its action at time t.

The localization problem is to determine the robot's location as a function of its observation history:

P(Loc_t | Obs₀, Act₀, Obs₁, Act₁, ..., Act_t-1,Obs_t).