Iterative-deepening A*
Iterative-Deepening A*
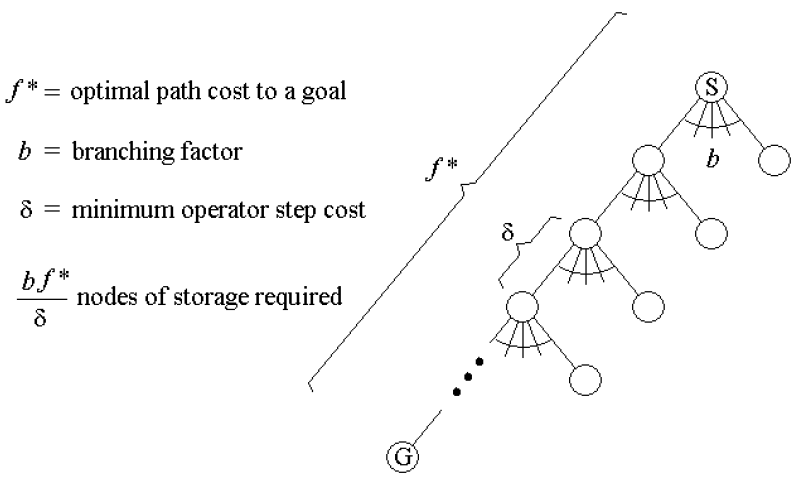
IDA* Algorithm: Iterative deepening A* or IDA* is similar to iterative-deepening depth-first, but with the following modifications: The depth bound modified to be an f-limit
1. Start with limit = h(start)
2. Prune any node if f(node) > f-limit
3. Next f-limit=minimum cost of any node pruned
The cut-off for nodes expanded in an iteration is decided by the f-value of the nodes.\
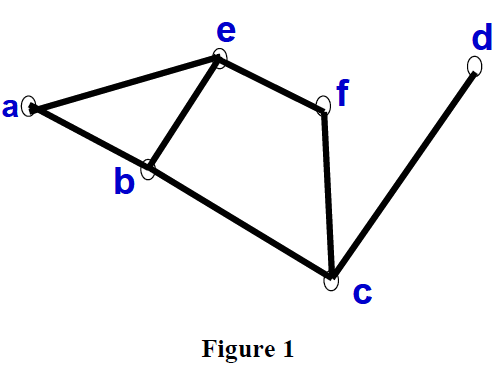
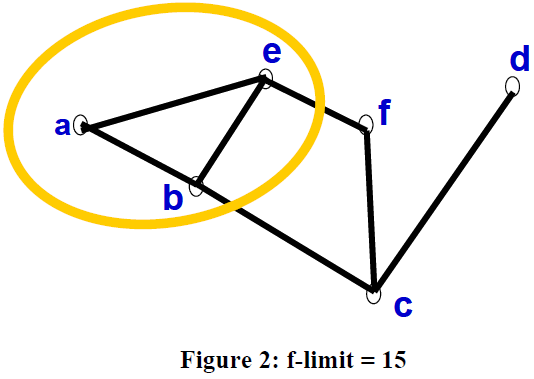
Consider the graph in Figure 3. In the first iteration, only node a is expanded. When a is expanded b and e are generated. The f value of both are found to be 15.
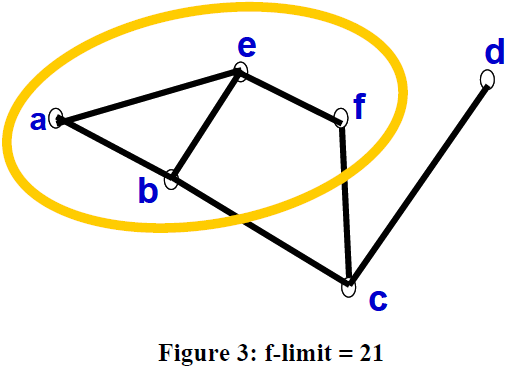
For the next iteration, a f-limit of 15 is selected, and in this iteration, a, b and c are expanded. This is illustrated in Figure 4.
IDA* Analysis: IDA* is complete & optimal Space usage is linear in the depth of solution. Each iteration is depth first search, and thus it does not require a priority queue. The number of nodes expanded relative to A* depends on unique values of heuristic function. The number of iterations is equal tit h number of distinct f values less than or equal to C*.
- In problems like 8 puzzle using the Manhattan distance heuristic, there are few possible f values (f values are only integral in this case.). Therefore the number of node expansions in this case is close to the number of nodes A* expands.
- But in problems like traveling salesman (TSP) using real valued costs, : each f value may be unique, and many more nodes may need to be expanded. In the worst case, if all f values are distinct, the algorithm will expand only one new node per iteration, and thus if A* expands N nodes, the maximum number of nodes expanded by IDA* is 1 2 … N = O(N2)
Why do we use IDA*? In the case of A*, it I usually the case that for slightly larger problems, the algorithm runs out of main memory much earlier than the algorithm runs out of time. IDA* can be used in such cases as the space requirement is linear. In fact 15-puzzle problems can be easily solved by IDA*, and may run out of space on A*.
IDA* is not thus suitable for TSP type of problems. Also IDA* generates duplicate nodes in cyclic graphs. Depth first search strategies are not very suitable for graphs containing too many cycles.
IDA* is complete, optimal, and optimally efficient (assuming a consistent, admissible heuristic), and requires only a polynomial amount of storage in the worst case: