Learning With Hidden Variables

Introduction: The preceding section dealt with the fully observable case. Many real-world problems have hidden variables (sometimes called latent variables) which are not observable in the data that are available for learning. For example, medical records often include the observed symptoms, the treatment applied, and perhaps the outcome of the treatment, but they seldom contain a direct observation of the disease itself!6 One might ask, “If the disease is not observed, why not construct a model without it?” The answer appears in Figure 20.7, which shows a small, fictitious diagnostic model for heart disease. There are three observable predisposing factors and three observable symptoms (which are too depressing to name). Assume that each variable has three possible values (e.g., none, moderate, and severe). Removing the hidden variable from the network in (a) yields the network in (b); the total number of parameters increases from 78 to 708. Thus, latent variables can dramatically reduce the number of parameters required to specify a Bayesian network. This, in turn, can dramatically reduce the amount of data needed to learn the parameters.

Hidden variables are important, but they do complicate the learning problem. In Figure 20.7(a), for example, it is not obvious how to learn the conditional distribution for HeartDisease, given its parents, because we do not know the value of HeartDisease in each case; the same problem arises in learning the distributions for the symptoms. This section

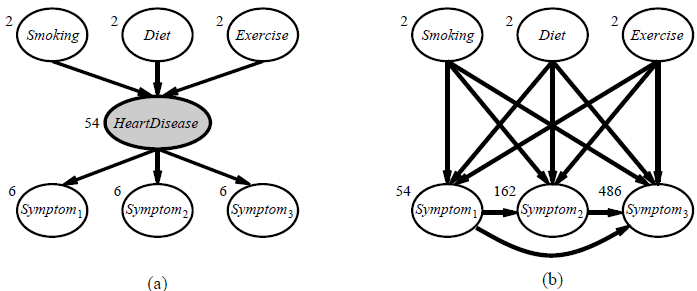
Figure 20.7 (a) A simple diagnostic network for heart disease, which is assumed to be a hidden variable. Each variable has three possible values and is labeled with the number of independent parameters in its conditional distribution; the total number is 78. (b) The equivalent network with HeartDisease removed. Note that the symptom variables are no longer conditionally independent given their parents. This network requires 708 parameters.

describes an algorithm called expectation–maximization, or EM, that solves this problem in a very general way. We will show three examples and then provide a general description. The algorithm seems like magic at first, but once the intuition has been developed, one can find applications for EM in a huge range of learning problems.