N-queens Eample

• Question: How do you avoid this local minima?

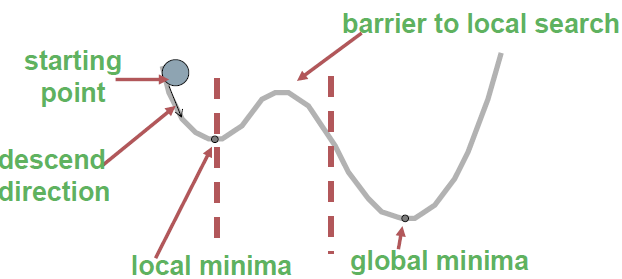
Consequences of Occasional Ascents
Simulated annealing: basic idea

• From current state, pick a random successor state;
• If it has better value than current state, then “accept the transition,” that is, use successor state as current state;

Simulated annealing: basic idea

• Otherwise, do not give up, but instead flip a coin and accept the transition with a given probability (that is lower as the successor is worse).
• So we accept to sometimes “un-optimize” the value function a little with a non-zero probability.
• Instead of restarting from a random point, we can allow the search to take some downhill steps to try to escape local maxima.
• Probability of downward steps is controlled by temperature parameter.
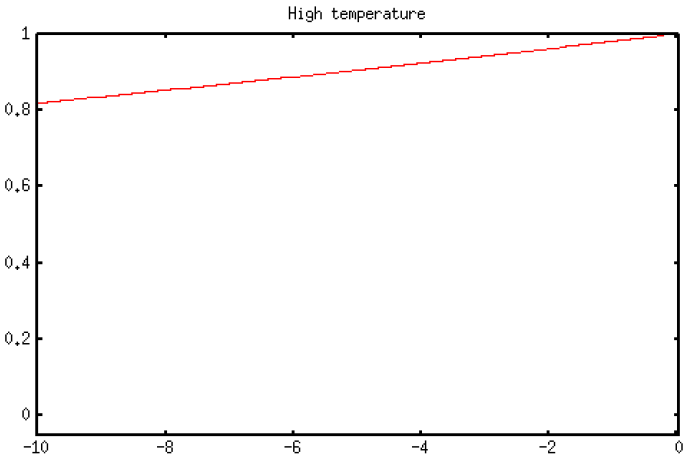
• High temperature implies high chance of trying locally "bad" moves, allowing nondeterministic exploration.
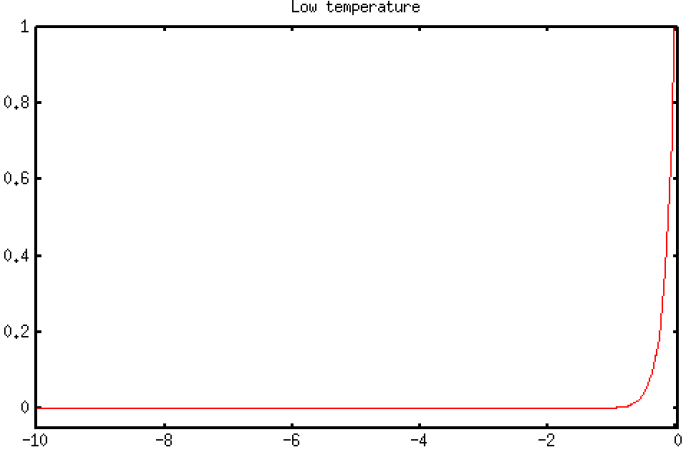
• Low temperature makes search more deterministic (like hill-climbing).
• Temperature begins high and gradually decreases according to a predetermined annealing schedule.
• Initially we are willing to try out lots of possible paths, but over time we gradually settle in on the most promising path.
• If temperature is lowered slowly enough, an optimal solution will be found.
• In practice, this schedule is often too slow and we have to accept suboptimal solutions.

Algorithm: set current to start state
for time = 1 to infinity {
set Temperature to annealing_schedule[time]
if Temperature = 0 {
return current
}
randomly pick a next state from successors of current
set ΔE to value(next) - value(current)
if ΔE > 0 {
set current to next
} else {
set current to next with probability eΔE/Temperature
}
}

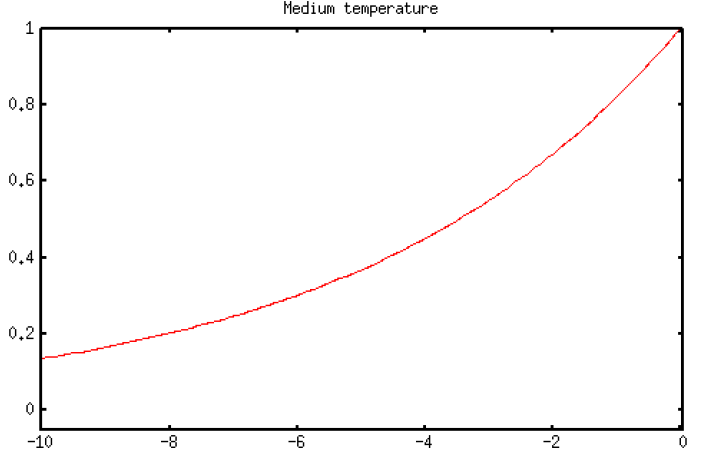
• Probability of moving downhill for negative ΔE values at different temperature ranges:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Other local search methods
• Genetic Algorithms