Naive Bayes Models

Naive Bayes models: Probably the most common Bayesian network model used in machine learning is the naive Bayes model. In this model, the “class” variable C (which is to be predicted) is the root and the “attribute” variables Xi are the leaves. The model is “naive” because it assumes that the attributes are conditionally independent of each other, given the class. (The model in Figure 20.2(b) is a naive Bayes model with just one attribute.) Assuming Boolean variables, the parameters are

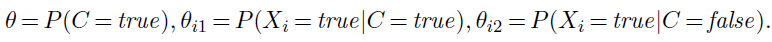
The maximum-likelihood parameter values are found in exactly the same way as for Figure 20.2(b). Once the model has been trained in this way, it can be used to classify new examples for which the class variable C is unobserved. With observed attribute values x1; : : : ; xn, the probability of each class is given by

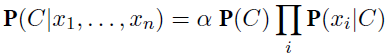
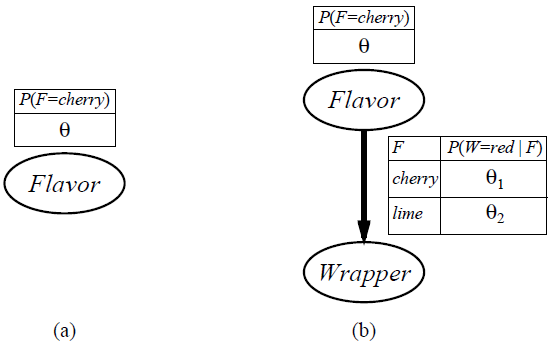
Figure 20.2 (a) Bayesian network model for the case of candies with an unknown proportion of cherries and limes. (b) Model for the case where the wrapper color depends (probabilistically) on the candy flavor.

A deterministic prediction can be obtained by choosing the most likely class. Figure 20.3 shows the learning curve for this method when it is applied to the restaurant problem. The method learns fairly well but not as well as decision-tree learning; this is presumably because the true hypothesis—which is a decision tree—is not representable exactly using a naive Bayes model.

Naive Bayes learning turns out to do surprisingly well in a wide range of applications; the boosted version is one of the most effective general-purpose learning algorithms. Naive Bayes learning scales well to very large problems: with n Boolean attributes, there are just 2n 1 parameters, and no search is required to find hML, the maximum-likelihood naive Bayes hypothesis. Finally, naive Bayes learning has no difficulty with noisy data and can give probabilistic predictions when appropriate.

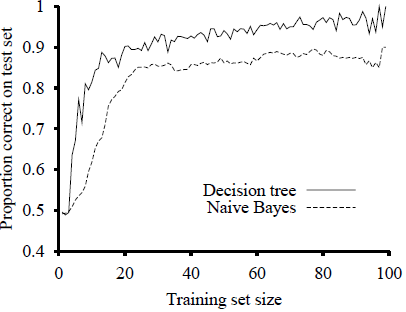
Figure 20.3 The learning curve for naive Bayes learning applied to the restaurant problem; the learning curve for decision-tree learning is shown for comparison.