Planning Systems

Planning Systems: Classical Planners use the STRIPS (Stanford Research Institute Problem Solver) language to describe states and operators. It is an efficient way to represent planning algorithms.

Representation of States and Goals: States are represented by conjunctions of function-free ground literals, that is, predicates applied to constant symbols, possibly negated.

An example of an initial state is:

At(Home) /\ -Have(Milk) /\ -Have(Bananas) /\ -Have(Drill) /\ ...

A state description does not have to be complete. We just want to obtain a successful plan to a set of possible complete states. But if it does not mention a given positive literal, then the literal can be assumed to be false. Goals are a conjunction of literals. Therefore the goal is

At(Home) /\ Have(Milk) /\ Have(Bananas) /\ Have(Drill)

Goals can also contain variables. Being at a store that sells milk is equivalent to

At(x) /\ Sells(x,Milk)

We have to differentiate between a goal given to a planner which is producing a sequence of actions that makes the goal true if executed, and a query given to a theorem prover that produces true or false if there is truth in the sentences, given a knowledge base.

We also have to keep track of the changes rather than of the states themselves because most actions change only a small part of the state representation.

Representation of Actions
Strips operators consist of three components

• action description: what an agent actually returns to the environment in order to do something.
• precondition: conjunction of atoms (positive literals), that says what must be true before an operator can be applied.
• effect of an operator: conjunction of literals (positive or negative) that describe how the situation changes when the operator is applied.

An example action of going from one place to another:

Op(ACTION:Go(there), PRECOND:At(here) /\ Path(here, there) EFFECT:At(there) /\ -At(here))

The following figure shows a diagram of the operator Go(there). The preconditions appear above the action, and the effects below.

Operator Schema: an operator with variables.

• it is a family of actions, one for each of the different values of the variables.
• every variable must have a value

Preconditions and Effects are restrictive. Operator o is applicable in a state s if every one of the preconditions in o are true in s. An example is if the initial situation includes the literals

At(Home, Path(Home, Supermarket)...

then the action Go(Supermarket) is applicable, and the resulting situation contains the literals

-At(Home),At(Supermarket), Path(Home, Supermarket)...

The result is all positive literals in Effect(o) hold, all literals in s hold and negative literals in Effect(o) are ignored. The set of operators for the “Box World” example problem is shown below:

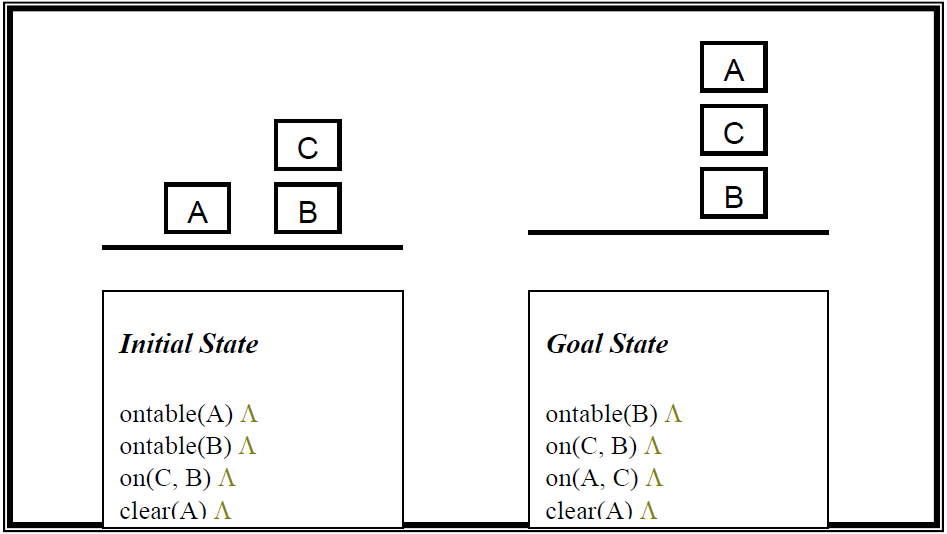
Definitions of Descriptors:

• ontable(x): block x is on top of the table
• on(x,y): block x is on top of block y
• clear(x): there is nothing on top of block x; therefore it can be picked up
• handempty: you are not holding any block

Definitions of Operators:

• Op{ACTION: pickup(x)
• PRECOND: ontable(x), clear(x), handempty
• EFFECT: holding(x), ~ontable(x), ~clear(x), ~handempty }
• Op{ACTION: putdown(x)
• PRECOND: holding(x)
• EFFECT: ontable(x), clear(x), handempty, ~holding(x) }
• Op{ACTION: stack(x,y)
• PRECOND: holding(x), clear(y)
• EFFECT: on(x,y), clear(x), handempty, ~holding(x), ~clear(y) }
• Op{ACTION: unstack(x,y)
• PRECOND: clear(x), on(x,y), handempty
• EFFECT: holding(x), clear(y), ~clear(x), ~on(x,y), ~handempty ) }