Proof Of Admissibility Of A*

Proof of Admissibility of A*: We will show that A* is admissible if it uses a monotone heuristic. A monotone heuristic is such that along any path the f-cost never decreases. But if this property does not hold for a given heuristic function, we can make the f value monotone by making use of the following trick (m is a child of n)
f(m) = max (f(n), g(m) h(m))
o Let G be an optimal goal state
o C* is the optimal path cost.
o G2 is a suboptimal goal state: g(G2) > C*
Suppose A* has selected G2 from OPEN for expansion.

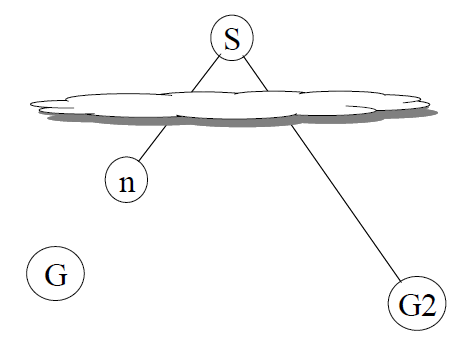
Consider a node n on OPEN on an optimal path to G. Thus C* ≥ f(n)
Since n is not chosen for expansion over G2, f(n) ≥ f(G2)
G2 is a goal state. f(G2) = g(G2)
Hence C* ≥ g(G2).
This is a contradiction. Thus A* could not have selected G2 for expansion before reaching the goal by an optimal path.

Proof of Completeness of A*
Let G be an optimal goal state. A* cannot reach a goal state only if there are infinitely many nodes where f(n) ≤ C*. This can only happen if either happens:
o There is a node with infinite branching factor. The first condition takes care of this.
o There is a path with finite cost but infinitely many nodes. But we assumed that Every arc in the graph has a cost greater than some ε> 0. Thus if there are infinitely many nodes on a path g(n) > f*, the cost of that path will be infinite.
Lemma: A* expands nodes in increasing order of their f values.

• A* is thus complete and optimal, assuming an admissible and consistent heuristic function (or using the pathmax equation to simulate consistency).
• A* is also optimally efficient, meaning that it expands only the minimal number of nodes needed to ensure optimality and completeness.

Performance Analysis of A*
Model the search space by a uniform b-ary tree with a unique start state s, and a goal state, g at a distance N from s.
The number of nodes expanded by A* is exponential in N unless the heuristic estimate is logarithmically accurate
|h(n) – h*(n)| ≤ O ( log h*(n) )

In practice most heuristics have proportional error. It becomes often difficult to use A* as the OPEN queue grows very large. A solution is to use algorithms that work with less memory.