Propositional Logic Inference
Propositional Logic Inference: Let KB = { S1, S2,..., SM } be the set of all sentences in our Knowledge Base, where each Si is a sentence in Propositional Logic. Let { X1, X2, ..., XN } be the set of all the symbols (i.e., variables) that are contained in all of the M sentences in KB. Say we want to know if a goal (aka query, conclusion, or theorem) sentence G follows from KB.
Model Checking: Since the computer doesn't know the interpretation of these sentences in the world, we don't know whether the constituent symbols represent facts in the world that are True or False. So, instead, consider all possible combinations of truth values for all the symbols, hence enumerating all logically distinct cases:

There are 2^N rows in the table.
- Each row corresponds to an equivalence class of worlds that, under a given interpretation, have the truth values for the N symbols assigned in that row.
- The models of KB are the rows where the third-to-last column is true, i.e., where all of the sentences in KB are true.
- A sentence R is valid if and only if it is true under all possible interpretations, i.e., if the entire column associated with R contains all true values.
- Since we don't know the semantics and therefore whether each symbol is True or False, to determine if a sentence G is entailed by KB, we must determine if all models of KB are also models of G. That is, whenever KB is true, G is true too. In other words, whenever the third-to-last column has a T, the same row in the second-to-last column also has a T. But this is logically equivalent to saying that the sentence (KB => G) is valid (by definition of the "implies" connective). In other words, if the last column of the table above contains only True, then KB entails G; or conclusion G logically follows from the premises in KB, no matter what the interpretations (i.e., semantics) associated with all of the sentences!
- The truth table method of inference is complete for PL (Propositional Logic) because we can always enumerate all 2^n rows for the n propositional symbols that occur. But this is exponential in n. In general, it has been shown that the problem of checking if a set of sentences in PL is satisfiable is NP-complete. (The truth table method of inference is not complete for FOL (First-Order Logic).)
Example: Using the "weather" sentences from above, let KB = (((P ^ Q) => R) ^ (Q => P) ^ Q) corresponding to the three facts we know about the weather: (1) "If it is hot and humid, then it is raining," (2) "If it is humid, then it is hot," and (3) "It is humid." Now let's ask the query "Is it raining?" That is, is the query sentence R entailed by KB? Using the truth-table approach to answering this query we have:

Hence, in this problem there is only one model of KB, when P, Q, and R are all True. And in this case R is also True, so R is entailed by KB. Also, you can see that the last column is all True values, so the sentence KB => R is valid.
Instead of an exponential length proof by truth table construction, is there a faster way to implement the inference process? Yes, using a proof procedure or inference procedure that uses sound rules of inference to deduce (i.e., derive) new sentences that are true in all cases where the premises are true. For example, consider the following:
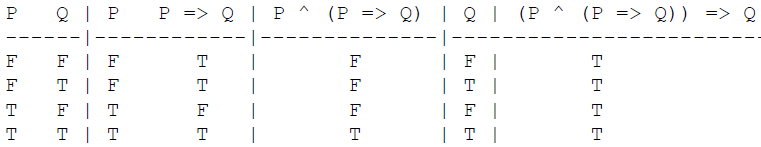
Since whenever P and P => Q are both true (last row only), Q is true too, Q is said to be derived from these two premise sentences. We write this as KB |- Q. This local pattern referencing only two of the M sentences in KB is called the Modus Ponens inference rule. The truth table shows that this inference rule is sound. It specifies how to make one kind of step in deriving a conclusion sentence from a KB.
Therefore, given the sentences in KB, construct a proof that a given conclusion sentence can be derived from KB by applying a sequence of sound inferences using either sentences in KB or sentences derived earlier in the proof, until the conclusion sentence is derived. This method is called the Natural Deduction procedure. (Note: This step-by-step, local proof process also relies on the monotonicity property of PL and FOL. That is, adding a new sentence to KB does not affect what can be entailed from the original KB and does not invalidate old sentences.)