Rules Of Inference

Rules of Inference: Here are some examples of sound rules of inference. Each can be shown to be sound once and for all using a truth table. The left column contains the premise sentence(s), and the right column contains the derived sentence. We write each of these derivations as A |- B , where A is the premise and B is the derived sentence.

In addition to the above rules of inference one also requires a set of equivalences of propositional logic like “A /\ B” is equivalent to “B /\ A”. A number of such equivalences were presented in the discussion on propositional logic.'

Using Inference Rules to Prove a Query/Goal/Theorem: A proof is a sequence of sentences, where each sentence is either a premise or a sentence derived from earlier sentences in the proof by one of the rules of inference. The last sentence is the query (also called goal or theorem) that we want to prove. Example for the "weather problem" given above.

Inference vs Entailmant: There is a subtle difference between entailment and inference.

Notice that inference is not directly related to truth; i.e. we can infer a sentence provided we have rules of inference that produce the sentence from the original sentences. However, if rules of inference are to be useful we wish them to be related to entailment. Ideally we would like:

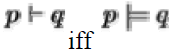
We have inferred q by applying rules of inference to p, but there is some model in which p holds but q does not hold. In this case the rules of inference have inferred ``too much''.

q is a sentence which holds in all models in which p holds, but we cannot find rules of inference that will infer q from p. In this case the rules of inference are insufficient to infer the things we want to be able to infer.