Soundness And Completeness

Soundness and Completeness: These notions are so important that there are 2 properties of logics associated with them.

``A sound inference procedure infers things that are valid consequences''

``A complete inference procedure is able to infer anything that is that is a valid consequence''
The ``best'' inference procedures are both sound and complete, but gaining completeness is often computationally expensive. Notice that even if inference is not complete it is desirable that it is sound.

Propositional Logic and Predicate Logic each with Modus Ponens as their inference produce are sound but not complete. We shall see that we need further (sound) rules of inference to achieve completeness. In fact we shall see that we shall even restrict the language in order to achieve an effective inference procedure that is sound and complete for a subset of First Order Predicate Logic.

The notion of soundness and completeness is more generally applied than in logic. Whenever we create a knowledge based program we use the syntax of the knowledge representation language, we assign a semantics in some way and the reasoning mechanism defines the inference procedures. The semantics will define what entailment means in this representation and we will be interested in how well the reasoning mechanism achieves entailment.

Decidability
Determining whether is computationally hard. If q is a consequence then if is complete then we know that and we can apply the rules of inference exhaustively knowing that we will eventually find the sequence of rules of inference. It may take a long time but it is finite.
However if q is not a consequence (remember the task is whether or not ) then we can happily apply rules of inference generating more and more irrelevant consequences. So the procedure is guaranteed to eventually stop if q is derivable, but may not terminate otherwise.

Entailment in Propositional Logic is decidable since truth tables can be applied in a finite number of steps to determine whether or not .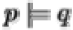
Entailment in Predicate Logic is only semi-decidable; it is only guaranteed to terminate when q is a consequence. One result of this semi-decidability is that many problems are not decidable; if they rely on failing to prove some sentence. Planning is typically not decidable. A common reaction to a non-decidable problem is to assume the answer after some reasoning time threshold has been reached. Another reaction to the semi-decidability of Predicate Logic is to restrict attention to subsets of the logic; however even if its entailment is decidable the procedure may be computationally expensive.