Splitting Functions

Splitting Functions: What attribute is the best to split the data? Let us remember some definitions from information theory.

A measure of uncertainty or entropy that is associated to a random variable X is defined as
H(X) = - Σ pi log pi
where the logarithm is in base 2.

This is the “average amount of information or entropy of a finite complete probability scheme”. We will use a entropy based splitting function. Consider the previous example:

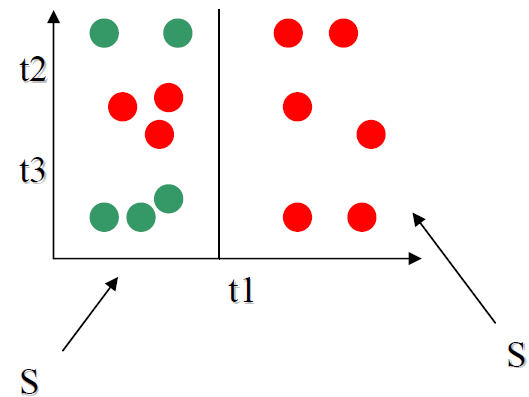
Size divides the sample in two.
S1 = { 6P, 0NP}
S2 = { 3P, 5NP}
H(S1) = 0
H(S2) = -(3/8)log2(3/8)
-(5/8)log2(5/8)

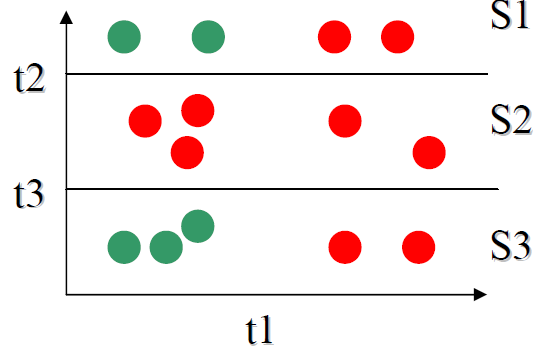
humidity divides the sample in three.
S1 = { 2P, 2NP}
S2 = { 5P, 0NP}
S3 = { 2P, 3NP}
H(S1) = 1
H(S2) = 0
H(S3) = -(2/5)log2(2/5)
-(3/5)log2(3/5)

Let us define information gain as follows:
Information gain IG over attribute A: IG (A)
IG(A) = H(S) - Σv (Sv/S) H (Sv)
H(S) is the entropy of all examples. H(Sv) is the entropy of one subsample after partitioning S based on all possible values of attribute A.

Consider the previous example:

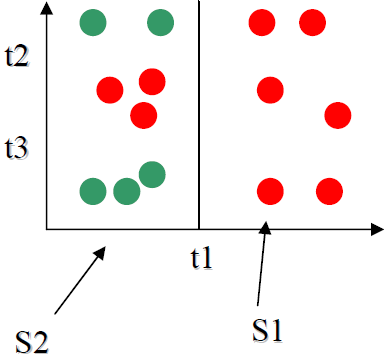
We have,
H(S1) = 0
H(S2) = -(3/8)log2(3/8)
-(5/8)log2(5/8)
H(S) = -(9/14)log2(9/14)
-(5/14)log2(5/14)
|S1|/|S| = 6/14
|S2|/|S| = 8/14
The principle for decision tree construction may be stated as follows: Order the splits (attribute and value of the attribute) in decreasing order of information gain.