Statistical Algorithms

Classification Algorithms: Classification algorithms are Statistical algorithms, having supervised learning and predicting categorical labels. Following are the few types of classification algorithms:

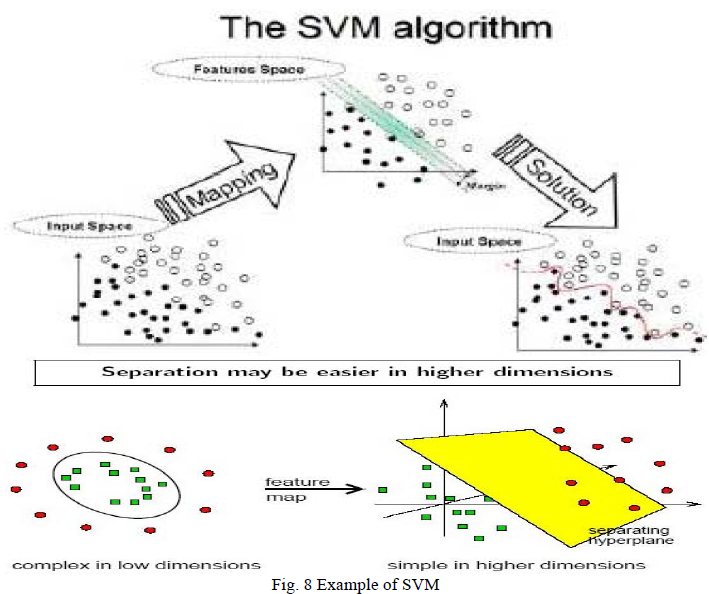
Support Vector Machines: A Support Vector Machine (SVM) performs classification by constructing an N-dimensional hyper plane that optimally separates the data into two categories. A support vector machine (SVM) is a concept in computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis. The standard SVM takes a set of input data and predicts, for each given input, which of two possible classes the input is a member of, which makes the SVM a non-probabilistic binary linear classifier. Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples into one category or the other. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible.

Neural Network (Multi Level Perceptron): Neural network is an interconnected network of neurons. It works on a concept of human brain system and possesses few traits like we can train ANN for best matched solution, ANN can perform fuzzy matching and provides optimal solution. ANN acts as a classifier in pattern recognition.

Kernel Estimation & K-nearest neighbor: In pattern recognition, the k-nearest neighbor algorithm (k-NN) is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbor algorithm is amongst the simplest of all machine learning algorithms: an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of its nearest neighbor.

Maximum Entropy Classifier: Maximum Entropy Classifier is a regression model which generalizes logistic regression by allowing more than two discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables (which may be real-valued, binary-valued, categorical-valued, etc.). Maximum entropy classifiers are commonly used as alternatives to Naive Bayes classifiers because they do not require statistical independence of the independent variables (commonly known as features) that serve as predictors.

Naive Bayes Classifier: A Naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem (from Bayesian statistics) with strong (naive) independence assumptions. A more descriptive term for the underlying probability model would be "independent feature model". In simple terms, a naive Bayes classifier assumes that the presence (or absence) of a particular feature of a class is unrelated to the presence (or absence) of any other feature. For example, a fruit may be considered to be an apple if it is red, round, and about 4" in diameter. Even if these features depend on each other or upon the existence of the other features, a naive Bayes classifier considers all of these properties to independently contribute to the probability that this fruit is an apple. Depending on the precise nature of the probability model, naive Bayes classifiers can be trained very efficiently in a supervised learning setting. In many practical applications, parameter estimation for naive Bayes models uses the method of maximum likelihood; in other words, one can work with the naive Bayes model without believing in Bayesian probability or using any Bayesian methods.