Unification

Unification

• Given two substitutions S = [t1/x1 .. tn/xn] and V = [u1/y1 .. um/ym], the composition of S and V, S . V, is the substitution obtained by:

1. Applying V to t1 .. tn [the operation on substitutions with just this property is called concatenation], and
2. adding any pair uj/yj such that yj is not in {x1 .. xn}.

For example: [G(x y)/z].[A/x B/y C/w D/z] is [G(A B)/z A/x B/y C/w]. Composition is an operation that is associative and non commutative

• A set of forms f1 .. fn is unifiable iff there is a substitution S such that f1.S = f2.S = .. = fn.S. We then say that S is a unifier of the set. For example {P(x F(y) B) P(x F(B) B)} is unified by [A/x B/y] and also unified by [B/y].
• A Most General Unifier (MGU) of a set of forms f1 .. fn is a substitution S that unifies this set and such that for any other substitution T that unifies the set there is a substitution V such that S.V = T. The result of applying the MGU to the forms is called a Most General Instance (MGI). Here are some examples:

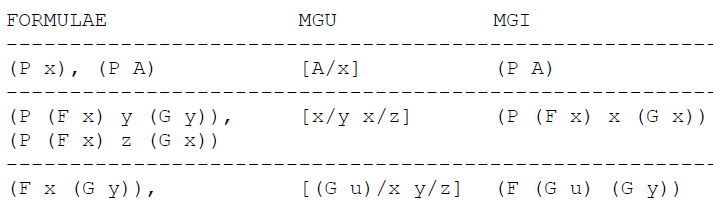
This last example is interesting: we first find that (G u) should replace x, then that (G z) should replace x; finally that x and z are equivalent. So we need x->(G z) and x->z to be both true. This would be possible only if z and (G z) were equivalent. That cannot happen for a finite term. To recognize cases such as this that do not allow unification [we cannot replace z by (G z) since z occurs in (G z)], we need what is called an Occur Test . Most Prolog implementation use Unification extensively but do not do the occur test for efficiency reasons.
The determination of Most General Unifier is done by the Unification Algorithm. Here is the pseudo code for it:

FUNCTION Unify WITH PARAMETERS form1, form2, and assign RETURNS MGU, where form1 and form2 are the forms that we want to unify, and assign is initially nil.

1. Use the Find-Difference function described below to determine the first elements where form1 and form2 differ and one of the elements is a variable. Call difference-set the value returned by Find-Difference. This value will be either the atom Fail, if the two forms cannot be unified; or null, if the two forms are identical; or a pair of the form (Variable Expression).
2. If Find-Difference returned the atom Fail, Unify also returns Fail and we cannot unify the two forms.
3. If Find-Difference returned nil, then Unify will return assign as MGU.
4. Otherwise, we replace each occurrence of Variable by Expression in form1 and form2; we compose the given assignment assign with the assignment that maps Variable into Expression, and we repeat the process for the new form1, form2, and assign.

FUNCTION Find-Difference WITH PARAMETERS form1 and form2 RETURNS pair, where form1 and form2 are e-expressions.

1. If form1 and form2 are the same variable, return nil.
2. Otherwise, if either form1 or form2 is a variable, and it does not appear anywhere in the other form, then return the pair (Variable Other-Form), otherwise return Fail.
3. Otherwise, if either form1 or form2 is an atom then if they are the same atom then return nil otherwise return Fail.
4. Otherwise both form1 and form2 are lists.
   Apply the Find-Difference function to corresponding elements of the two lists until either a call returns a non-null value or the two lists are simultaneously exhausted, or some elements are left over in one list.
   In the first case, that non-null value is returned; in the second, nil is returned; in the third, Fail is returned