Ambiguity
Ambiguity: The grammar given by
G = ({S},{a, b}, S, S ® aSb | bSa | SS | l) generates strings having an equal number of a’s and b’s.
The string “abab” can be generated from this grammar in two distinct ways, as shown in the following derivation trees:
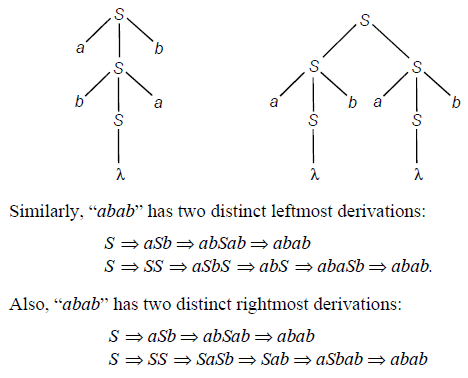
Each of the above derivation trees can be turned into a unique rightmost derivation, or into a unique leftmost derivation. Each leftmost or rightmost derivation can be turned into a unique derivation tree. These representations are largely interchangeable.
Ambiguous Gram mars/Ambiguous Languages: Since derivation trees, leftmost derivations, and rightmost derivations are equivalent rotations, the following definitions are equivalent:
Definition: LetG = (N,T, P, S ) be a CFG. A string wÎL(G) is said to be “ambiguously derivable “if there are two or more different derivation trees for that string in G.
Definition: A CFG given by G = (N, T, P, S) is said to be “ambiguous” if there exists at least one string in L(G) which is ambiguously derivable. Otherwise it is unambiguous.
Ambiguity is a property of a grammar, and it is usually, but not always possible to find an equivalent unambiguous grammar. An “inherantly ambiguous language” is a language for which no unambiguous grammar exists.
Example 1: Prove that the grammar
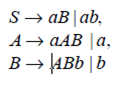
is ambiguous.
Solution: It is easy to see that “ab” has two different derivations as shown below. Given the grammar G with production