Axiomatization Of Propositional Logic

Axiomatization of Propositional Logic: We now present one axiomatization of propositional calculus following the Hilbert style. Let the syntax of well-formed formulas (wff) be as follows:

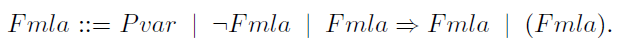
In other words, a formula is a propositional variable, the negation of a propositional formula, an implication formula, or a parenthesized for mula. This grammar defines a complete set of formulas in the sense that all Boolean propositions can be expressed in it (prove this assertion). Following Church, a Hilbert calculus for propositional logic can be set up based on three axioms (A1-A3) and two rules of inference (R1-R2) shown below. Here, p and q stand for propositional formulas.

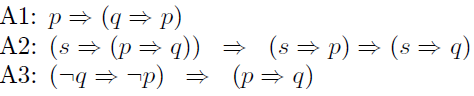
R1 (Modus Ponens): If P is a theorem and P ⇒ Q is a theorem, conclude that Q is a theorem.
Example: From p and p ⇒ (p ⇒ q), infer p ⇒ q. R2 (Substitution): The substitution of wffs for propositional variables in a theorem results in a theorem. A substitution is a “parallel assignment” in the sense that the newly introduced formulas themselves are not affected by the substitution (as would happen if, for instance, the substitutions are made serially).
Example: Substituting (p ⇒ q) for p and (r ⇒ p) for q in formula p ⇒ q, results in (p ⇒ q) ⇒ (r ⇒ p). It is as if p and q are replaced by fresh and distinct variables first, which, in turn, are replaced by (p ⇒ q) and (r ⇒ p) respectively. We do not perform the substitution of r ⇒ p for q first, and then affect the p introduced in this process by the substitution of (p ⇒ q) for p.
Given all this, a proof for a simple theorem such as p ⇒ p can be carried out – but it can be quite involved:

P1: From A1, through substitution of p ⇒ p for q, we obtain

p ⇒ ((p ⇒ p) ⇒ p).
P2: From A2, substituting p for s, p ⇒ p for p, and p for q, we obtain
(p ⇒ ((p ⇒ p) ⇒ p)) ⇒ (p ⇒ (p ⇒ p)) ⇒ (p ⇒ p).
P3: Modus ponens between P1 and P2 yields
(p ⇒ (p ⇒ p)) ⇒ (p ⇒ p).
P4: From A1, substituting p for q, we obtain
p ⇒ (p ⇒ p).
Modus ponens between P4 and P3 results in (p ⇒ p).

It is straightforward to verify that the above axiomatization is sound. This is because the axioms are true, and every rule of inference is truth-preserving. The axiomatization is also complete, as can be shown via a proof by induction. The take away message from these discussions is that it pays to hone the axiomatization of a formal logic into something that is parsimonious as well as enjoys the attributes of being sound, complete, and independent, as explained earlier.