Basic Operations On Bdds
Basic Operations on BDDs: BDDs are capable of efficiently representing transition relations of finite-state machines. In some cases, transition relations of finite-state machines that have of the order of 2100 states have been represented using BDDs. For example, a BDD that represents the transition relation for a 100-bit digital ripple-counter can be built using about 200 BDD nodes.7 Such compression is, of course, achieved by implicitly representing the state space; an explicit representation (e.g., using pointer based data structures) of a state-space of this magnitude is practically impossible. Given a transition relation, one can perform forward or backward reachability analysis. ‘Forward reachability analysis’ is the term used to describe the act of computing reachable states by computing the forward image (“image”) of the current set of states (starting from the initial states). Backward reachability analysis computes the pre-image of the current set of states. One typically starts from the current set of states violating the desired property, and attempts to find a path back
to the initial state. If such a path exists, it indicates the possibility of a computation that violates the desired property.
Each step in reachability analysis takes the current set of states represented by a BDD and computes the next set of states, also represented by a BDD. It essentially performs a breadth-first traversal, generating each breadth-first frontier in one step from the currently reached set of states. The commonly used formulation of traversal is in terms of computing the least fixed-point as explained in Section 11.3.2. When the least fixed-point is reached, one can query it to determine the overall properties of the system. One can also check whether desired system invariants hold in an incremental fashion (without waiting for the fixed-point to be attained) by testing the invariant after each new breadth-first frontier has been generated. Here, an invariant refers to a property that is true at every reachable state. We will now take up these three topics in turn, first illustrating how we are going to represent state transition systems.
Representing state transition systems
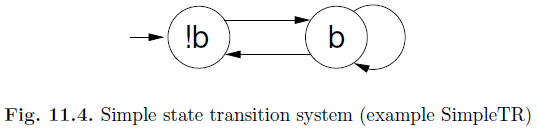
We capture transition systems by specifying a binary state transition relation between the current and next states, and also specifying a predicate capturing the initial states. If inputs and outputs are to be modeled, they are made part of the state vector. Depending on the problem being modeled, we may not care to highlight which parts of the state vector are inputs and which are outputs. In some cases, the entire state of the system will be captured by the states of inputs and outputs. Figure 11.4 presents an extremely simple state transition system, called SimpleTR. Initially, the state is 0. Whenever the state is 0, it can become 1. When it is 1, it can either stay 1 or become 0. These requirements can be captured using a single Boolean variable b representing the current state, another Boolean variable b representing the next state,8 and an initial state predicate and a state transition relation involving these variables, as follows:
The initial state predicate for SimpleTR is λb.¬b, since the initial state is 0. Often, instead of using the lambda syntax, initial state predicates are introduced by explicitly introducing a named initial state predicate I and defining it by an equation such as I(b) = ¬b. For brevity,9 we shall often say “input state represented by ¬b.”
The state transition relation for SimpleTR is λ(b, b).¬bb bb b¬b , where each product term represents one of the transitions. The values of b and b for which this relation is satisfied represent the present and next states in our example. In other words,
– amovewhere b is false now and true in the next state is represented by ¬bb'.
– a move where b is true in the present and next states is represented by bb'.
– finally, a move where b is true in the present state and false in the next state is represented by b¬b'.
This expression can be simplified to λ(b, b).(b b ). The above relation can also written in terms of a transition relation T defined as T(b, b ) = b b'. We shall hereafter say “transition relation b b'.” Notice that this transition relation is false for b = 0 and b = 0, meaning there is no move from state 0 to itself (all other moves are present).
Forward reachability: The set of reachable states in SimpleTR starting from the initial state ¬b can be determined as follows:
- Compute the set of states in the initial set of states.
- Compute the set of states reachable from the initial states in n steps, for n = 1, 2, . . ..
In other words, we can introduce a predicate P such that a state x is in P if and only if it is reachable from the initial state I through a finite number of steps, as dictated by the transition relation T. The above recursive recipe is encoded as
P(s) = (I(s) ∨ ∃x.(P(x) ∧ T(x, s))).
This formula says that s is in P if it is in I, or there exists a state x such that x is in P, and the transition relation takes x to s. Rewriting the above definition, we have
P = λs.(I(s) ∨ ∃x.(P(x) ∧ T(x, s)))).
Rewriting again, we have
P = (λG.(λs.(I(s) ∨ ∃x.(G(x) ∧ T(x, s))))) P.
In other words, P is a fixed-point of
λG.(λs.(I(s) ∨ ∃x.(G(x) ∧ T(x, s)))).
Let us call this Lambda expression H:
H = λG.(λs.(I(s) ∨ ∃x.(G(x) ∧ T(x, s)))).
In general, H can have multiple fixed-points. Of these, the least fixedpoint represents exactly the reachable set of states, as next explained in next Section.
Fixed-point iteration to compute the least fixed-point: As we know the least fixed-point can be obtained by “bottom refinement” using the functional obtained from the recursive definition. In the same manner, we will determine P, the least fixed-point of H, by computing its approximants that, in the limit, become P. Let us denote the approximants P0, P1, P2, . . .. We have P0 = λx.false, the “everywhere false” predicate. The next approximation to P is obtained by feeding P0 to the “bottom refiner”:
P1 = λG.(λs.(I(s) ∨ ∃x.(G(x) ∧ T(x, s))))P0
which becomes λs.I(s). This approximant says that P is a predicate true of s whenever I(s). While this is not true (P must represent the reachable state set and not the initial state alone), it is certainly a better answer than what P0 denotes, which is that there are no states in the reachable state set! We now illustrate all the steps of this computation, taking SimpleTR for illustration. We use the abbreviation of not showing the lambda abstracted variables in each step.