Boolean Satisfiablity

BOOLEAN SATISFIABILITY: Assume we have n Boolean variables, viz., A, B, C, .... and an expression in the propositional Calculus i.e., we can use and, or and not to form the expression.

Is there an assignment of truth values to the variables, (for example, A = true, B = true, C = false), that will make the expression true?

Here is a nondeterministic algorithm to solve the problem: For each Boolean variable, assign if the proper truth value. This is a linear algorithm. We can find a deterministic algorithm for this problem in much the same way as we did for the integer bin problem. Effectively, the idea is to set up a systematic procedure to try every possible assignment of truth values to variables. The algorithm terminates when a satisfactory solution is found, or when all 2n possible assignments have been tried. Again, the deterministic solution requires exponential time.

Example 1: Check whether the boolean formula

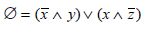
is satisfiable or not.

Solution: A Boolean formula is satisfiable if some assignment of 0s and 1s to the variables makes the formula evaluate to 1.

When x = 0, y = 1 and z = 0, we have

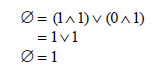
Therefore the Boolean formula is satisfiable.