Church-turing Thesis

CHURCH–TURING’S THESIS: Alan Turing defined Turing machines in an attempt to formalize the notion of an “effective producer” which is usually called as ‘algorithm’ these days. Simultaneously mathematicians were working independently on the same problem.

Emil Post -> Production Systems

Alonzo Church -> Lambda Calculus

Noam Chomsky ->Unrestricted Grammars

Stephen Kleene -> Recursive function Theory

Raymond Smullyn -> Formal Systems.

All of the above formalisms were proved equivalent to one another. This led to

(a) Turing’s Thesis (Weak Form): A Turing machine can compute anything that can be computed by a general-purpose digital computer.

(b) Turing’s Thesis (Strong Form): A Turing machine can compute anything that can be computed.

The strong form of Turing’s Thesis cannot be proved it states a relationship between mathematical concepts and the “real world”.

Counting: Two sets can be put into a one-to-one corresponding if and only if they have exactly the same number of elements.

Recursive and Recursively Enumerable Language: There are three possible outcomes of executing a Turing machine over a given input.

The Turing machine may

Halt and accept the input
Halt and reject the input, or
Never halt.

A language is “recursive” if there exists a Turing machine that accepts every string of language and rejects every string over the same alphabet that is not in the language. If a language L is recursive, then its complement L should also be recursive.

A language is “recursively enumerable” if there exists a Turing machine that accepts every string of the language, and does not accept strings that are not in the language. Strings which are not in the language may be rejected or may cause the Turing machine to go into an infinite loop.

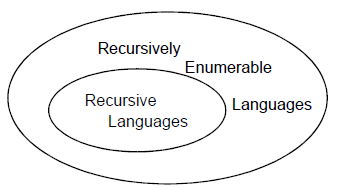
Every Recursive language is also recursively enumerable. But it is not clear if every recursively enumerable language is also recursive.

Turing Machines are not “recursive”. The terminology is borrowed from recursive function theory.