Closure Properties Of Regular Languages

THEOREM 1: If L1 and L2 are regular over S, then L1 L2 È is regular i.e., union of two regular sets is also regular. [Regular sets are closed w.r.t. union].

Proof: As L1 and L2 are given to be regular; there exists finite automata M1 Q 1 q1 F1 = ( , S,d , , ) and M2 Q2 2 q2 F2 = ( , S,d , , ) such that

L1 = T(M1) and

L2 = T (M2).

[T (M) = {x ÎS* : d(q , x)ÎF} is a language L(M) accepted by M]

Let us assume that Q1 ÇQ2  = Æ.

Let us define NFA with Î-transitions as follows:

M3 Q q0 F = ( , S,d, , )

where

1. Q = Q ÈQ È q 1 2 { 0} where q0 is a new state not in Q1 ÈQ2
2. F = F È F 1 2
3. d is defined byd(q0 ,∈) {q1 , q2}                                        (a)

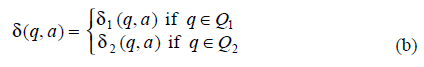
It is obvious that d(q0 , ) {q1 , q2} Î = induces Î-transitions either to the initial state q1 of M1 or initial state q2 of M2.

From (b), the transitions of M are the same as transitions M1 or M2 depending on whether q1 or q2 reached by Î-transitions from q0.

Since F = F È F 1 2, any string accepted by M1 or M2 accepted by M. Therefore L1 L2 T M È = ( ) and so is reg ular. ¨

THEOREM 2: If L is regular and L Í S* , then S* - L is also a regular set.

Proof: Let L = T(M) where M = (Q, S,d, q , F ) 0 is an FA.

Though L Í S*, d (q, a) need not be defined as for all ‘a’ in S. d (q, a) is defined for some ‘a’ in S even though ‘a’ does not find a place in the strings accepted by M.

Let us now modify S, Q and d as defined below.

1. If a ÎS - S 1 , then the symbol ‘a’ will not appear in any string of T(M). Therefore we delete ‘a’ from S1 and all transitions defined by the symbol ‘a’. T(M) is not affected by this).
2. If S - S ¹Æ 1 , we add a dead state d to Q. We define d(d, a) = d for all ‘a’ in S and d(d, a) = d for all q in Q and ‘a’ in S - S1 .

Once again T (M) is not affected by this.

Let us consider M got after applying (i) and (ii) to S,Q and d. We write the modified M as

(Q, S, d, q , F ).

Let us now define a new automaton M¢ by

M¢ = (Q, S,d, q ,Q - F ) 0 .

We can see that wÎT (M¢ ) iff d(q0 , w) Q F Î - and wÏT (M).

Therefore  S* - L = T (M¢ ) and therefore regular.

THEOREM 3: If L1 and L2 are regular, so is L1 L2 Ç [Regular sets are closed w.r.t. Intersection]

Proof: It is important to note that

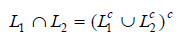
If L1 and L2 are regular, then L^c₁, L^c₂are regular by theorem 1.

Therefore 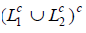is regular by theorem 2.

Hence L1 ÇL2is regular.