Complete Language And Functions
COMPLETE LANGUAGES AND FUNCTIONS: A Turing machine has an output function, the contents of the input tape after processing, a given input string can be viewed as the result of computation. Therefore a Turing machine is seen as a computer of functions, from integers to integers.
Let us now look at the procedure to compute functions f (n1 , n2 ,. . . nk ) where n1 , n2 , . . . , nk are non-negative integers.
(a) Represent the integers n1 , n2 , KK , nk in unary i.e., n1 is written as 0n1 etc. The input (n1 , n2 ,., nk ) is represented by 0n110n2. . . 10nkwhere the 1’s are used to separate the unary representation of n1 , n2 , . . . . , nk .
(b) After several moves, if the Turing Machine halts (either in a final state or in any other state) and has 0m in the input tape, then F (n1 , n2 , . . . . , nk ) = m.
Example 4.2.1: Design a Turing machine to add two given integers.
Solution: Assume that m and n are positive integers. Let us represent the input as 0mB0n. If the separating B is removed and 0’s come together we have the required output, m n is unary.
- The separating B is replaced by a 0.
- The rightmost 0 is erased i.e., replaced by B.
Let us define M = ({q0 , q1 , q2 , q3 , q4},{0},{0, B},d, q0 ,{q4}). d is defined by Table shown below.
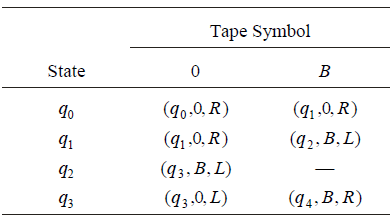
M starts from ID q0mB0n, moves right until seeking the blank B. M changes state to q1. On reaching the right end, it reverts, replaces the rightmost0 by B. It moves left until it reaches the beginning of the input string. It halts atthe final state q4.
Example 2: Design a Turing Machine that multiplies two positive integers in unary notation.
Solution:
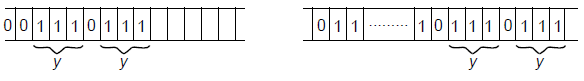
Assume that the initial and final tape contents are to be as indicated in figure above. Multiplication is visualized as a repeated copying of the multiplicand y for each 1 in the multiplies x, whereby the string y is added the appropriate number of times to the partially computed product. The steps involved in the process are:
- Repeat the following steps until x contains no more 1’s—find a 1 in x and replace it with another symbol a. Replace the leftmost 0 by 0y.
- Replace all a’s with 1’s.