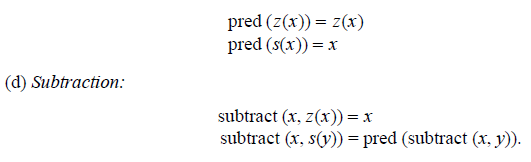Composition And Recursion

COMPOSITION AND RECURSION: If g1, g2, g3 and h are previously defined functions, these functions can be combined to form new functions. These functions can be combined only in precisely defined ways.

(a) Composition: f (x, y) = h(g (x, y), g (x, y)) 1 2 . This allows us to use functions as arguments to functions.

(b) Primitive Recursion: This is a structured “recursive routine” with the form:

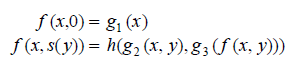
“A primitive recursive function is a function formed from the functions z, s, p1 and p2 by using only composition and primitive recursion”.

The recursion should be guaranteed to terminate. In order to ensure this, the function should carry along an extra parameter that is “decremented” every time the function is called [s(x) replaced by x], and halts the recursion when it reaches “zero” (z(x)), i.e., f z x

The recursive function should appear only once in the definitions (RHS of the definition). This in fact, avoids various forms of “fancy” recursion.

Examples:The following examples show how these can be used to define more complicated functions.

(a) Addition of two numbers: According to the form, it is:

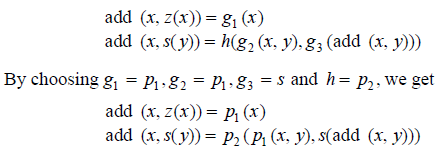
which simplifies to

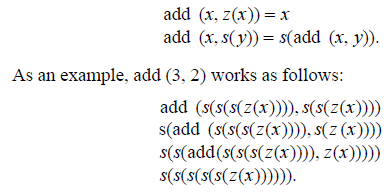
(b) Multiplication of Two Numbers: The new feature is the use of a previously defined function, add, in the definition of a new function. We skip the step of playing around with the pi functions to pick out the right parts, and go to the simplified form.

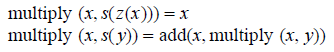
(c) Predecessor of a Number: The important catch here is that it will not be able to drop below zero, so effectively 0 – 1 = 0. In order to show this, we write a dot above the minus sign and call it “monus”. The function is easy to define: