Computations Vs. Computation Trees

Computations vs. computation trees: In general, it is not sufficient to view the behavior of a system in terms of computational sequences, such as captured by waveforms. To see why, consider Figure 22.2, where two scenarios of a user interacting with a machine (say, a vending machine) are shown in the top and bottom half. In each scenario, the behavior shown to the left of the " sign is that of the vending machine, while the behavior shown to the right of the " sign is that of the human customer. The upper vending machine accepts a coin-drop (shown as a), and decides to allow the user to bang open its trap door (b). Since there are two (nondeterministic) ways to open the trap door, the user may be faced with a candy (c) or a donut (d) – never both at the same time! Since the user is always insistent on collecting a candy (c) after a b event, the system will deadlock if the machine chooses d instead of a c. Unfortunately, these “internal choices” made by the machine cannot3 often be controlled from outside, and so such machines do exist in real life. The machine in the bottom half is not

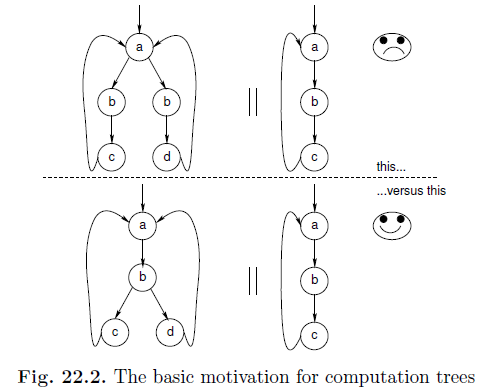
prone to this deadlock, as it always leaves c and d enabled after a b. How does one model this subtle, but important difference between the two machines? Modeling the finite behaviors of the machines through regular expressions, one obtains (ab(c d))∗ as the regular expression for both machines — and so the use of regular expressions does not help distinguish the machines.
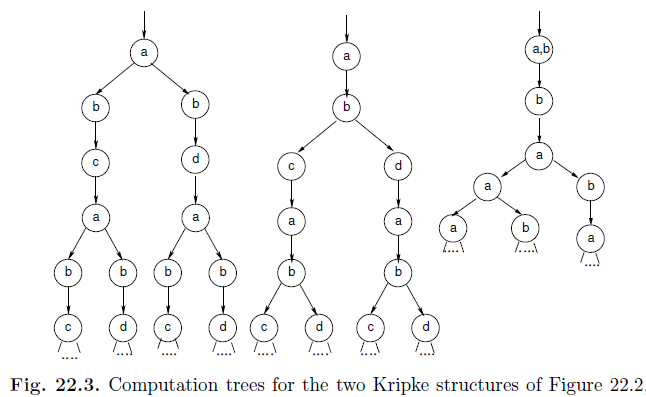
Let us therefore take another approach to see how we can distinguish these machines. In this approach, we unwind the machines into their infinite computation trees, as shown in Figure 22.3 for the Kripke structures of Figure 22.2 and the left-hand side Kripke structure of Figure 22.1. With these computation trees at hand, one can then ask questions such as:
“At all times, after seeing a b event being offered, does there exist a path leading into a future where the c event is guaranteed to be offered?”
It is clear that the Kripke structures of Figure 22.2 are distinguished by this query: the bottom machine provides this guarantee by always allowing the user to pull out c, while the top machine might sometimes precommit to offering only a d. Computational tree logic (CTL) considers not only the truths of atomic propositions along paths as linear-time temporal logic (LTL) does, but also has the ability to consider: (i) whether there exists (E) paths at a state that satisfy a given criterion, or whether for all (A) paths at a state, some criterion holds. However, this is not to say that CTL is superior to LTL. There are many path-centered properties such as fairness that are expressible only in LTL and not in CTL.