Connectives

Illustration

(i)  If p : I am clever

and q : You are strong

then pÚ q = I am clever or you are strong.

Mathematicians have settled on “Inclusive or”: pÚ q means p is true or q is true or both are ture.

(ii)  If p : The butler did it.

and q : The cook did it. then we have

pÚ q: either the butler or the cook did it.

(iii) If p : The butler did it

q : The cook did it

r : The lawyer did it, then we have

( pÚ q) Ù (~ r): Either the but ler or the cook did it, but not the lawyer.

(d)    Implication (Conditional/ if ........ then):The conditional pÞq, read as “if p, then q” or “p implies q”, is defined by the following truth table.

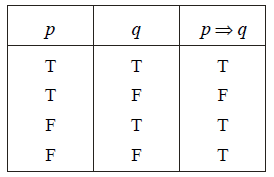
The arrowÞ is the “conditional” operator, and in pÞq the statement p is called the “antecedent” or “hypothesis”, and q is called the “consequent”, or “conclusion”.

Illustration

(i) If p and q are both true, then pÞq is true. For example, “if 2 2 = 4, then the sun rises in the East”

Here: p : “2 2 = 4” and q : “the sun rises in the east”.

(ii) If p is true and q is false, then pÞq is false. For example:

“When it rains, I carry an umbrella”. Here p : It is raining; q : I carry an umbrella.

If it is raining then I carry an umbrella. Now there are lot of days when it rains (p is true) and I forget to bring my umbrella (q is false). On any of those days the statement pÞq is clearly false.

(e)    Biconditional (If and only if........):The Biconditional  pÛq, which is read as “p if and only if p” or “p is equivalent to q” is defined by the following truth table.

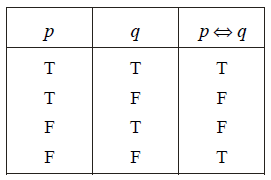
From the truth table, we see that for pÛq to be true, both p and q must have the same truth values; otherwise it is false.

The statement pÛq is defined to be the statement ( pÞq) Ù (q Þ p).

For this reason, the double headed arrow Û is called the “biconditional”. Each of the following is equivalent to the biconditional pÛq

(i) p if and only if q

(ii) p is necessary and sufficient for q.

(iii) p is equivalent to q.