Conversion Of Nfa To Dfa

Introduction: Conversion of The NFA simpliﬁes computational design, but the use of nondeterministic selections and ǫ-transitions makes it look very diﬀerent from FA.An NFA for a language can be smaller and easier to construct than a DFA.

A Greedy Conversion Algorithm

Step 1: For each state p ∈ Q and for each symbol a ∈Σ, compute the set R(p, a) of all states that can be reached from state p by:

(a) any number of ǫ transitions,

(b) one transition labeled by a, and then

Step 2: Initialize the state collection S as {p0}, where p0 is the set of all states that can be reached from q0 by following any number of ǫ transitions.

Step 3: While S contains a state with no outgoing edges, select an arbitrary member, say r, of S, and do the following:

• For each symbol a, compute the state ra as ∪q∈rR(q, a), add ra to S if ra is not already in it, and then draw an arc from r to ra.

Algorithm Execution Example:

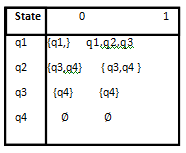
Step 2: Initially S = {{q1}}.

Step 3: {q1} on 0 changes the state to {q1}

{q1} on 1 changes the state to {q1, q2, q3}. New!

{q1, q2, q3} on 0 changes the state to {q1, q3, q4}. New!

{q1, q2, q3} on 1 changes the state to {q1, q2, q3, q4}. New!

{q1, q3, q4} on 0 changes the state to {q1, q4}. New!

{q1, q2, q3} on 1 changes the state to {q1, q2, q3, q4}.

{q1, q2, q3, q4} on 0 changes the state to {q1, q3, q4}.

{q1, q2, q3, q4} on 1 changes the state to {q1, q2, q3, q4}.

{q1, q4} on 0 changes the state to {q13}.

{q1, q4} on 1 changes the state to {q1, q2, q3}.