Derivation Tree

Introduction: A ‘derivation tree’ is an ordered tree which the the nodes are labeled with the left sides of productions and in which the children of a node represent its corresponding right sides.

Definition of a Derivation Tree: Let G = (V, T, S, P) be a CFG. An ordered tree is a derivation tree for G iff it has the following properties:

1. The root of the derivation tree is S.
2. Each and every leaf in the tree has a label from T È{l}.
3. Each and every interior vertex (a vertex which is no a leaf) has a label from V.
4. If a vertex has label AÎV, and its children are labeled (from left to right) a1 , a2 , . .  an , then P must contain a production of the form A -> a1, a2, an,. . .
5. A leaf labeled l has no siblings, that is, a vertex with a child labeled l can have no other children.

Sentential Form: For a given CFG with productions S ® aA, A® aB, B® bB, B® a. The derivation tree is as shown below.

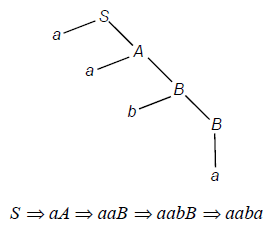
The resultant of the derivation tree is the word w = aaba. This is said to be in “Sentential Form”.

Partial Derivation Tree: In the definition of derivation tree given, if every leaf has a label from V ÈT È{l} it is said to be “partial derivation tree”.

Right Most/Left Most/Mixed Derivation

Consider the grammar G with production

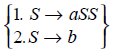
Now, we have

The sequence followed is “left most derivation”, fol lowing “1121222”, giving “aababbb”.

The sequence 1212122 represents a “Mixed Derivation”, giving “aababbb”.

The sequence 1211222 represents a “Right Most Derivation”, giving “aababbb”.