Deterministic Finite State Automaton (Dfa)
Automata: An automaton is an abstract model of a digital computer. An automaton has a mechanism to read input, which is a string over a given alphabet. This input is actually written on an “input file”, which can be read by the automaton but cannot change it.
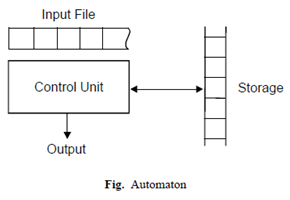
Input file is divided into cells, each of which can hold one symbol. The automaton has a temporary “storage” device, which has unlimited number of cells, the contents of which can be altered by the automaton. Automaton has a control unit, which is said to be in one of a finite number of “internal states”. The automaton can change state in a defined way.
Types of Automaton
(a) Deterministic Automata
(b) Non-deterministic Automata
A deterministic automata is one in which each move (transition from one state to another) is unequally determined by the current configuration. If the internal state, input and contents of the storage are known, it is possible to predict the future behavior of the automaton. This is said to be deterministic automata otherwise it is non-determinist automata.
An automaton whose output response is “yes” or “No” is called an “Acceptor”.
Definition of Deterministic Finite Automaton
A Deterministic Finite Automator (DFA) is a 5-tuple
M = (Q, S,d, q , F ) 0
where
Q = Finite state of “internal states”
S = Finite set of symbols called “Input alphabet”
d :Q ´ S®Q = Transition Function
q0 Q Î = Initial state
FÍ Q = Set of Final states
The input mechanism can move only from left to right and reads exactly one symbol on each step. The transition from one internal state to another are governed by the transition function d. If d(q0 , a) q1 , = then if the DFA is in state q0 and the current input symbol is a, the DFA will go into state q1.
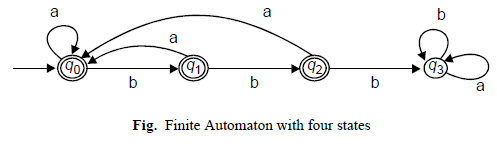
Example: Design a DFA, M which accepts the language L(M) = {wÎ(a, b)* :w does not contain three consecutive b’s).
Let M = (Q, S, d, q , F )
where
Q = {q0, q1, q2, q3}
S = {a, b}
q0 is the initial state
F = {q0, q1, q2,} are initial states and d is defined as follows:
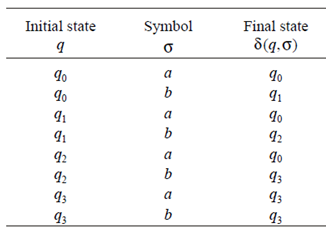
Solution: M does not accept specified language, as long as three consecutive b’s have not been read. It should be noted that
(i) M is in state qi (where i = 0,1, or 2) immediately after reading a run of i consecutive b’s that either began the input string or was preceded by an ‘a’.
(ii) If an ‘a’ is read and M is in state, q0, q1, or M returns to its initial state q0.
q0, q1 and q2 are “Final states” (as given in the problem). Therefore any input string not containing three consecutive b’s will be accepted.
In case we get three consecutive b’s then the q3 state is reached (which is not final state), hence M will remain in this state, irrespective of any other symbol in the rest of the string. This state q3 is said to be “dead state” or M is said to be “trapped” at q3.
The DFA schematic is shown below based on the discussion above.