Dicision Algorithms

DECISION ALGORITHMS

THEOREM: Given L is a regular set, i.e., a language accepted by a finite automaton. There exists a constant ‘n’ such that if ‘s’ in any string in L and | s| ³ n, then s = uvw such that | uv| £ n, | v| ³1 and for all i ³ 0, uv iwÎL.

Proof: Let us assume that L = T(M) where M = (Q, S,d, q , F ) 0 and ‘n’ be the number of states in Q.

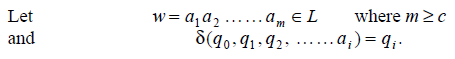
Since m ³ n, the number of states, the sequences q0 , q1 ,. . . .qm will have some repeated states. Hence there are two integers j and k, 0 £ j < k < n such that qi = qk. Let us assume that k is least in the chosen pair (j, k). For this we have

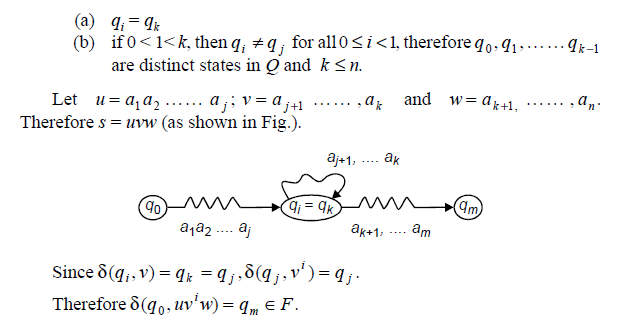
This illustrates that uv ^IwÎL, for all i ³ 0.

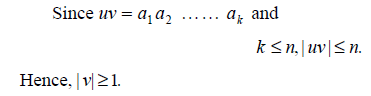
THEOREM: The set of strings that is accepted by a finite automaton which has ‘n’ state is

• nonempty if and only if M accepts some string of length less than n.
• infinite, if an only if M accepts some string of length k where

n £ k < 2n.

Thus there is a DECISION ALGORITHM, to find out whether M accepts zero, a finite number, or an infinite number of strings.

Algorithm (i): Let us give an algorithm to decide if T (M) = Æ.

Let us consider the strings of length less than n. Test if any of these strings is in T(M). If so, T (M) = Æ. Otherwise, T(M) is empty.

Algorithm (ii): Let us give an algorithm to decide if T(M) is infinite.

Let us consider the strings of length k, where n £ k £ 2n -1. Test if any such string is found in T(M). If so, T(M) is infinite, otherwise T(M) is finite.

Exam ple 3.4.1: Prove that there exists an algorithm to find if two finite

automata M1 and M2 accept the same language.

Proof: Let us assume that

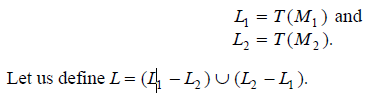
The language L is regular.

Let us assume that M is a finite automaton such that L = T(M).

Now, if L = Æ, iff L1= L2  .

Since there is an algorithm (decision algorithm) to test if L is a empty, we have an algorithm to check if L1 = L2.