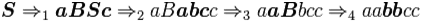Grammar
Introduction: In 1959, Noam Chomsky tried to give a mathematical definition for grammar. The motivation was to give a formal definition for grammar for English sentences. He defined four types of grammar viz., type 0, type 1, type 2, and type 3. At the same time, the programming language ALGOL was being considered. It was considered as a block-structured language and a grammar was required which could describe all syntactically correct programs. The definition given was called Backus Normal Form or Backus-Naur Form (BNF). This definition was found to be the same as the definition given by Chomsky for type 2 grammar.
We now formally define the four types of grammars:A context-free grammar G is defined by the 4-tuple:
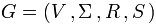Where
1. v is a finite set; each element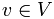 
is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by G.
2. Σ is a finite set of terminals, disjoint from V, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar G.
3. R is a finite relation from V to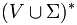 
, where the asterisk represents the Kleene star operation. The members of R are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a P)
4. S is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of V.
The semantics of grammars: The operation of a grammar can be defined in terms of relations on strings:
§ Given a grammar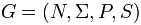 
, the binary relation => G (pronounced as "G derives in one step") on strings in 
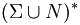is defined by:
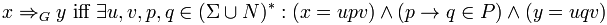
§ the relation => G* (pronounced as G derives in zero or more steps) is defined as the reflexive transitive closure of => G
§ a sentential form is a member of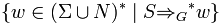 
that can be derived in a finite number of steps from the start symbol S; that is, a sentential form is a member of 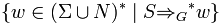. A sentential form that contains no nonterminal symbols (i.e. is a member of Σ*) is called a sentence.
§ The language of G, denoted as L(G), is defined as all those sentences that can be derived in a finite number of steps from the start symbol S; that is, the set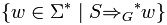 
.
Note that the grammar 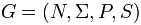is effectively the semi-Thue system
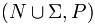, rewriting strings in exactly the same way; the only difference is in that we distinguish specificnonterminal symbols which must be rewritten in rewrite rules, and are only interested in rewritings from the designated start symbol S to strings without nonterminal symbols.
Example: For these examples, formal languages are specified using set-builder notation.
Consider the grammar G where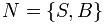
, 
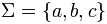, S is the start symbol, and P consists of the following production rules:
1. 
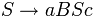
2. 
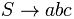
3. 
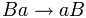
4. 
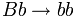
This grammar defines the language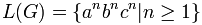 
where an denotes a string of n consecutive a's. Thus, the language is the set of strings that consist of 1 or more a's, followed by the same number of b's, followed by the same number of c's. Some examples of the derivation of strings in L(G) are:
§
§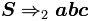