Introduction To Context-free Grammars

Definition of CFG: A context-free grammar is a 4-tuple (V, T, S, P) where

1. V is a finite set called the variables
2. T is a finite set, disjoint from V, called the terminals
3. P is a finite set of rules, with each rule being a variable and a string of variables and terminals, and
4. S ÎV is the start variable.

If u, v and w are strings of variables and terminals, and A-> w is a rule of the grammar, we say that uAv yields uwv, written uAv Þuwv.

Example of CFG: Given a grammar G = ({S}, {a, b}, R, S). The set of rules R is

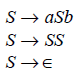
This grammar generates strings such as

abab, aaabbb, and aababb

If we assume that a is left parenthesis ‘(’ and b is right parenthesis ‘)’, then L(G) is the language of all strings of properly nested parentheses.

Right-Linear Grammar: In general productions have the form:

(V ÈT ) -> (V ÈT )* .

In right-linear grammar, all productions have one of the two forms:

V ->T *V

or V ->T *

i.e., the left hand side should have a single variable and the right hand side consists of any number of terminals (members of T) optionally followed by a single variable.

Right-Lin ear Gram mars and NFAs: There is a simple connection between right-linear grammars and NFAs, as shown in the following illustration.

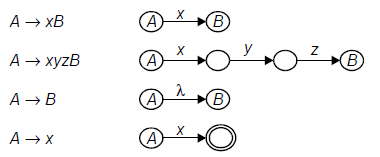
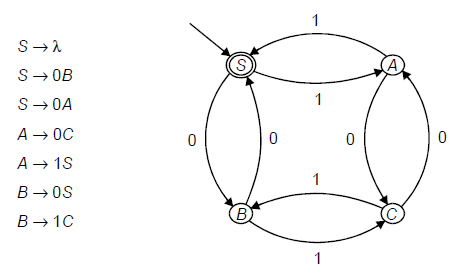
As an example of the correspondence between an NFA and a right linear grammar, the following automaton and grammar both recognize the set of set of strings consisting of an even number of 0’s and an even number of 1’s.

Left-Linear Grammar

In a left-linear grammar, all productions have one of the two forms:

• V ->VT *
• or V ->T *

i.e., the left hand side must consist of a single varibale, and the right-hand side consists of an optional single variable followed by one number of terminals.