Ltl Vs. Ctl Through An Example

LTL vs. CTL through an example: The differences between LTL and CTL are actually quite subtle. Consider Figure 22.4, and the CTL formula AG (EFx). In order for

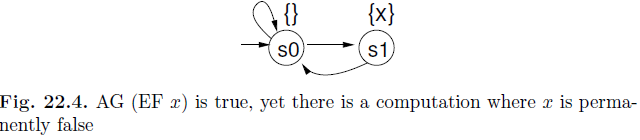
this formula to be true over this Kripke structure, in all paths starting from s0, everywhere along those paths, EFx must be true. This, in turn, means that there must exist a path where x is eventually found. Starting either from s0 or s1, we see that there exists a path on which x is found true eventually. Hence, AG (EFx) is true of this Kripke structure.
Let us try to pretend that the CTL formula AG (EF x) is equivalent to the LTL formula G (F x). An LTL formula is true of a Kripke structure if and only if it is true of every infinite path in the Kripke structure considered separately! Now consider the infinite path of spinning in state s0. For this infinite path, ¬x is permanently true. Therefore, we will violate Fx, and hence G (Fx). In short, this one path serves as the “death knell” for G (F x) with respect to this Kripke structure—whatever other paths might exist in this Kripke structure.