Machines

Introduction: All the machines discuss in the Power diagram, including DFAs, are primarily string processors. They are started in their initial state and are fed an input string. The inputs of interest are finitely long (“finite”) strings. The main question of interest is whether, at the end of the input, the machine is in an accepting state or not. The Turing machine has, in addition to a set of accepting states, a set of rejecting states.

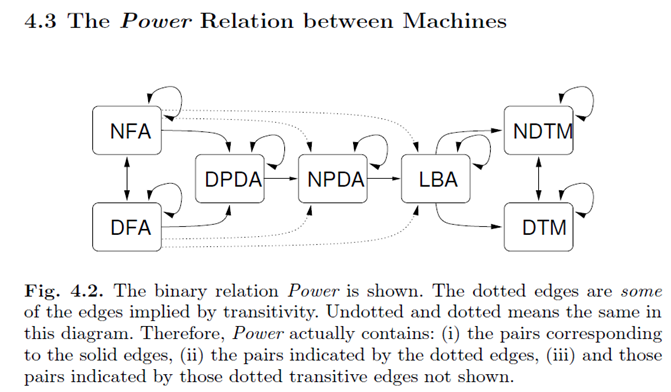
There are several axes along which machines can be distinguished. Some of these distinctions are now pointed out. We will remind the reader of these details when specific machine types are discussed. The purpose of the current discussion is to portray the overall nature of the variations that exist among machines.

All machine types in the Power diagram that are of lower power than the LBA (namely the DFA, NFA, DPDA, and NPDA) must read their input strings completely before it is deemed that they accept the input string. Furthermore, they must read their input string in the process of a single left-to-right scan (meaning, they cannot go back and reread a previously read symbol). In each step of computation, these machines are allowed to read atmost one input symbol (they may read none, as well).
The remaining machine types in the Power diagram, namely the LBA, DTM, and the NDTM, are not required to read the whole input on their input “tape.” In other words, it is possible for these machines to accept an input without having read all of it—or for that matter,1without having read any of it! Furthermore, they are allowed to reread a previously read input. This rereading may happen in any order (i.e., not confined to the order in which inputs are laid out on the tape).
All the machines in the Power diagram possess a finite-state control flow graph describing their behavior. The NFA, NPDA, and NDTMallow non-determinism in their control flow graph (non-determinism isdescribed in the next section). While the DFA and NFA are totallydescribed in terms of this finite-state control, the remaining machinetypes carry an additional data structure in the form of a stack or one ormore tapes. The DPDA and NPDA have access to a single unboundedstack from which they pop a single symbol at every step. Additionally,in each step, zero or more symbols may be pushed back onto the stack.
The LBA, the DTM, as well as the NDTM have, in addition to a control flow graph, a single read/write tape. There is the notion of a current position on this input tape, usually specified by the position of a read/write “head.” Also, there is the notion of presenting the input string over a contiguous sequence of cells on the input tape. The LBA is allowed to write a tape cell only if this cell belongs to the contiguous sequence of cells over which the initial tape input was presented. A Turing machine has no such restriction.

Note that we avoid depicting the Buchi automaton in the Power diagram of Chapter 3, as this machine type is not comparable withthese other machine types. For example, one can simulate an LBAon a Turing machine, or a DFA on a push-down automaton; no suchsimulation of the B¨uchi automata on any of the machines in the Power diagram is possible. In a sense, the presentation of B¨uchi automata isa way of making the reader aware of the existence of these machinesand the practical uses that these machines have in modeling time inan abstract manner, as well as broaden the reader’s perspective earlyon. Details on B¨uchi automata appear in Chapters 22 and 23. It is alsoimportant to point out that due to space/time limitations, we have leftout many machine types on finite strings that could easily have been depicted on the Power diagram, such as two-way automata [108]. Many of these machine have been proved equivalent to machines in the Powerdiagram, as far as the class of languages they recognize is concerned.

With this general introduction, we proceed to examine the various machine types beginning with the DFA.