Myhill-nerode Theorem-1

Myhill-Nerode Relations

Isomorphism: Two DFAs given by M QM m sm Fm = ( , S,d , , ) and N QN n sn Fn = ( , S,d , , ) are said to be “isomorphic” if there is a one-to-one and onto mapping

f : QM ®QN such that

1. f (sM ) = sN ,
2. (d M ( p, a)) = d N ( f ( p), a) for all P QM a Î , ÎS,
3. p FM if f p FN Î ( )Î .

Isomorphic automata accept same set.

Myhill-Nerode Relations: Let R Í S* be a regular set, and let M = (Q, S,d, s, F ) be a DFA for R with no inaccessible states.

The automaton M induces an equivalence relation º M on S* defined by

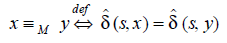
It is easy to show that the relation º M is an equivalence relation, meaning it is reflexive, symmetric and transitive.

A few properties satisfied by º M are as follows:

(a) It is a right congruence: for any x, yÎS* and a ÎS,

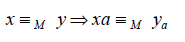
Proof: Assume x º _M y.

Therefore we have

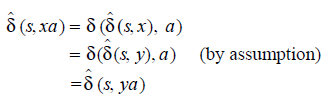
 (b) It refines R : for any x, yÎS* ,

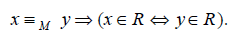
Proof: Since d$ (s, x) = d$ (s, y), which is either an accept state or a reject state, so either both x and y are accepted or both are rejected.

 

(c) It is of “Finite index”: i.e., it has only finitely much equivalence class.

This is because there is exactly one equivalence class

{x ÎS* | d$ (s, x) = q}

Corresponding to each state q of M.

Hence the equivalence relation º on S* is a “Myhill-Herode relation” for R if it satisfies properties (a), (b) and (c). i.e., if it is a right congruence of finite index refining R.

Myhill-Nerode Theorem: Let R Í S* . The following statements are equivalent.

1. R is regular
2. There exists a Myhill-Nerode relation for R
3. The relation º R is of finite index.

Example 1: Using Myhill-Nerode Theorem verify whether L = {a nbn : n ³ 0} is regular or not.

Solu tion: This is done by determining the º R -classes. If k ¹ m, then 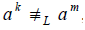since

a k bk ÎL but a mbk ÏL. Hence there are infinitely many º L -classes, at least one for each a k , k ³ 0. Hence by Myhill-Nerode Theorem L is not regular. (The application of Myhill-Nerode theorem has been illustrated above).