Nondeterministic Finite Automaton

Introduction: An input string is accepted by a nondeterministic finite automaton if and only if at least one of the possible transition sequences, defined by the input, leads to a final state. As language recognizer devices, nondeterministic automata are not more powerful than their deterministic counterpart, indeed they accept the same class of languages, that is to say they are equivalent. However, they are very often more convenient to use. In many cases, the most direct formalization of a problem is in terms of a nondeterministic automaton.

A NFA is represented formally by a 5-tuple, (Q, Σ, Δ, q0, F), consisting of

a finite set of states Q

a finite set of input symbols Σ

a transition relation Δ : Q × Σ → P(Q).

an initial (or start) state q0 ∈ Q

a set of states F distinguished as accepting (or final) states F ⊆ Q.

Example:An NFA that accepts all strings over {0, 1} that contain a 1 either at the third position from the end or at the second position from the end.

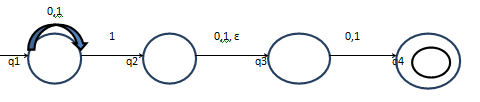
• There are two edges labeled 1 coming out of q1.
• There are no edges coming out of q4.
• The edge from q2 is labeled with ǫ, in addition to 0 and 1

Explanation of example:

• If the node you are in has an outgoing edge labeled ǫ, you may choose to follow it.

 After receiving a symbol,

• if the node you are in has multiple outgoing edges labeled with the symbol, you nondeterministically choose one of them and cross it;
• If there are no choices, stop there.

Transition Function for the Example

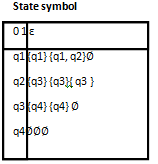
This NFA accepts y = 11 with respect to state sequence (q1, q2, q3, q4) and decomposition y = 1ε1.