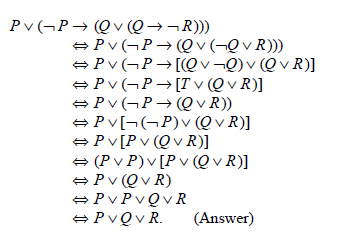Normal Forms

NORMAL FORMS: Let us show how to find the formula given the Truth Table.

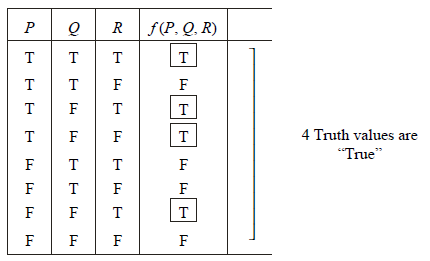
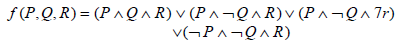
Formula obtained here is a “disjunction” of terms, each of which is a “conjunction” of “statement variables” and their “negations”. A product of statement variables and their negations is called “elementary production”. A sum of variables and their negations is called “elementary sum”.

Disjunctive Nor mal Form: A formula which is equivalent to a given formula and which has a sum of elementary products is called “disjunctive Normal Form” of the formula.

Conjunctive Nor mal Form: A formula which is equivalent to a given formula and that has a product of elementary sums is called “conjunctive Normal form” of the formula.

Procedure to find disjunctive Normal form

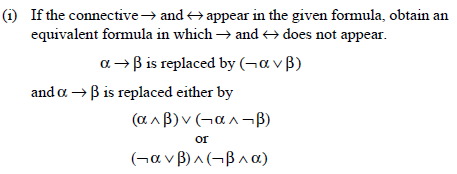
(ii) Using DeMorgan’s laws, an equivalent formula can be obtained in which the negation is applied to statement variables only, if the negation applied to a formula or part of the formula which is not a statement variable.

(iii) Applying the distributive law until a sum of elementary products is obtained.

This is the “Disjunctive Normal Form”, after applying the Idempotent law and suitable re-ordering. In the Normal Form, the elementary products which are equivalent to “F” (False), if any, can be ommitted.

Example 1: Obtain a disjunctive normal form of

Solution: