Npda To Cfg
NPDA to CFG
(a) We have shown that for any CFG, an equivalent NPDA can be obtained. We shall show also that, for any NPDA, we can produce an equivalent CFG. This will establish the equivalence of CFGs and NFDAs.
We shall assert without proof that any NPDA can be transformed into an equivalent NPDA which has the following form:
- The NPDA has only one final state, which it enters if and only if the stack is empty.
- All transitions have the form
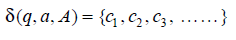
where each ci has one of the two forms

(b) When we write a grammar, we can use any variable names we choose. As in programming languages, we like to use “meaningful” variable names.
When we translate an NPDA into a CFG, we will use variable names that encode information about both the state of the NPDA and the stack content variable names will have the form
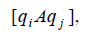
The “meaning” of the variable [qi Aqj] is that the NPDA can go from state qi with Ax on the stack to state qj with x on the stack. qi with Ax on the stack to state qj with x on the stack. Each transition of the form d(qi , a, A) (q j , l) = results in a single grammar rule. Each transition of the form
d(qi , a, A)= {q j , BC)
results is a multitude of grammar rules, one for each pair of states qx and qy in the NPDA.
Deterministic Pushdown Automata: A Non-deterministic finite acceptor differs from a deterministic finite acceptor in two ways:
(i) The transition function d is single-valued for a DFA, but multi-valued for an NFA.
(ii) An NFA may have l-transitions.
A non-deterministic pushdown automaton differs from a pushdown automaton in the following ways:
- The transition function d is at most single-valued for a DPDA, multi-valued for an NPDA. Formally: |d(q1 , a, b)| = 0 or1, for every q ÎQ, a ÎS È{l}, and bÎG.
- Both NPDA and DPDA may have l-transitions; but a DPDA may have a l-transition only if no other transition is possible. Formally: If |d(q, l, b)| ¹Æ, then d(q, c, b) = Æ for every cÎS.
A deterministic CFL is a language that can be recognized by a DPDA. The deterministic context-free languages are a proper subset of the context-free languages.