Pitfalls To Avoid

Pitfalls to Avoid: Let us do another example that points out a real pitfall. Consider the formulas Ff = ∀x.∃y.(x − y) = 1 and Ft = ∀y.∃x.(x − y) = 1. Over
natural numbers, Ff is false (consider x = 0) while Ft is true. Following the method for DFA construction all the way through, however,

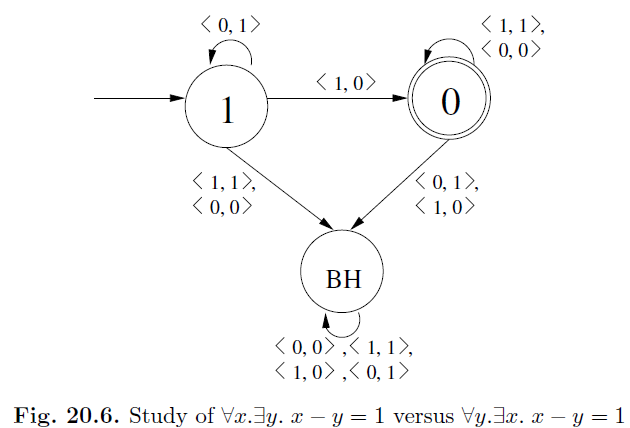
Figure 20.6 (which only represents the common matrix of these formulas) will reduce to the same machine with empty language as shown in Figure 20.5. In other words, our reasoning shows that Ff and Ft are false.

The restriction of equal bit-vector lengths: Let us think a bit more carefully about how the DFA construction method treats the matrix x−y = 1. This DFA is based on the following conventions:

• Bit-sequences are to be interpreted in unsigned binary. For example, 1 represents the value 1 in decimal while 11 represents 3 in decimal.
• We will accept x and y bit serially with the number of bits of x and y seen at any stage being equal. Suppose we have seen n 1s corresponding to y. What should be the n-long bit sequence corresponding to x such that x − y = 1? We immediately realize that there is no such x!

Therefore, we have to read ∀y.∃x.(x − y) = 1 as
∀y.∃x.[(x − y) = 1 ∧ eqlen(x, y)],
where eqlen is a predicate that asserts that the bit-serial vectors modeling x and y have the same length. With this interpretation, both formulas emerge false. In other words, for any run of y’s of all 1s (equal in magnitude to 2n − 1 for various n), there is no run of x of the same length that exceeds this magnitude.