Polynomial Time Algorithm

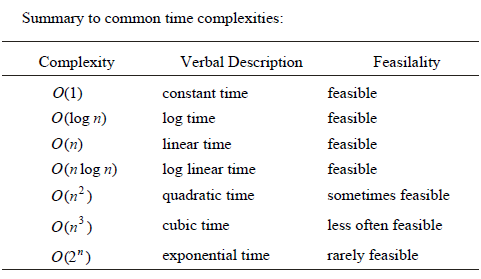
POLYNOMIAL-TIME ALGORITHMS: A polynomial-time algorithm is an algorithm whose execution time is either given by a polynomial on the size of the input, or can be bounded by such a polynomial. Problems which can be solved by a polynomial-time algorithm are called “tractable” problems. As an example, most algorithms on arrays can use the array size, n, as the input size. In order to find the largest element in any array requires a single pass through the array, so the algorithm which does this is of O(n), or it is a “linear time” algorithm.

Sorting algorithms take O(n log n) or O(n2) time. Bubble sort takes linear time in the least case, but O(n2) time in the average and worst cases. Heapsort takes O(n log n) time in all cases. Quicksort takes O(n log n) time on average, but O(n2) time in the worst case.

As far as O(n log n) is concerned, it must be noted that the base of the logarithms is irrelevant, as the difference is a constant factor, which is ignored. All programming tasks we know have polynomial solutions. It is not due to the reason that all practical problems have polynomial-time solutions.

Rather, it is because the day-to-day problems are one for which there is no known practical solution.

NON-DETERMINISTIC POLYNOMIAL TIME ALGORITHMS: A nondeterministic computation is viewed as:

1. when a choice point is reached, an infallible oracle can be consulted to determine the right option.
2. When a choice point is reached, all choices are made and computation can proceed simultaneously.

A Non-deterministic Polynomial Time Algorithm is one that can be executed in polynomial time on a nondeterministic machine. The machine can either consult an oracle in constant time, or it can spawn an arbitrarily large number of parallel processes, which is obviously a nice machine to have.

INTEGER BIN PACKING

Assume we are given a set of n integers. Our task is to arrange these integers into two piles or bins, so that the sum of the integers in one pile is equal to the sum of the integers in the other pile.

For example, given the integers

{19, 23, 32, 42, 50, 62, 77, 88, 89, 105, 114, 123, 176}

• These numbers sum to 1000. Can they be divided into two bins, bin A and bin B, such that the sum of the integers in each bin is 500?
• There is an obvious nondeterministic algorithm: For each number, put it in the correct bin. This requires linear time.
• There is also a fairly easy deterministic algorithm. There are 13 numbers (n = 13), so form the 13-bit binary number 0000000000000.

For i ranging from 1 to 13: if bit i is zero, put integer i into bin A; if bit i is one, put integer i into bin B. Test the resultant arrangement.

If we don’t have a solution yet, add 1 to the binary number and try again. If we reach 1111111111111, we will stop and conclude that there is no solution. This is fairly simply algorithm; the only problem is that it takes O(2n) time, that is, “exponential time”. In the above example, we may need to try as many as 213 arrangements. This is fine for all small values of n (such as 13), but becomes unreasonable for large values of n.

We could find many shortcuts for problems such as this, but the best we can do is improve the coefficients. The time complexity remains O(2n). Problems that require exponential time are referred to as “Intractable” problems.

There are many variants to this problem.

• We can have multiple bins.
• We can have a single bin, and the object is to pack as much as possible into it.
• We can pack objects with multiple dimensions (volume and weight, for example).