Proof Sketch Of The Undecidability Of Pcp

Proof sketch of the undecidability of PCP: The basic idea behind the proof of undecidability of PCP is to use ATM and the computation history method. In particular,

• Given a Turing machine M, we systematically go through the transition function δ of M as well as the elements of its tape alphabet, Γ, and generate a finite set of tiles, TilesM.
• Now we turn around and ask for an input string w that is in the initial tape of M. Then, with respect to M and w, we generate one additional tile, tileMw. We define Tiles = TilesM ∪ {tileMw}.
• We arrange it so that any solution to Tiles must begin with tileMw. This is achieved by putting special additional characters around the top and bottom rows of each tile, as will soon be detailed.
• We then prove that Tiles has one solution, namely SolnTiles, exactly when M accepts w. If M does not accept w, Tiles will have no solutions, by construction. Furthermore, SolnTiles would end up being a sequence t1, t2, . . . , tk such that when the tiles are lined up according to this solution, the top and bottom rows of the tiles would, essentially,5 be the accepting computation history of M on w.
• Hence, given a solver for PCP, we can obtain a solver for ATM.

The crux of achieving the above reduction is to generate each set of tiles carefully; here is how we proceed to generate the members of Tiles.6 Here, the following notations are used: if u is the string of characters u1u2 . . .un,

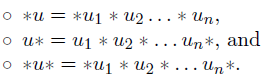
In Figure 17.2, we illustrate the encoding ideas behind the PCP undecidability proof through the example of a Turing machine starting from state p with its tape containing string 0100 — i.e., ID p01. This Turing machine firstmoves one step right to ID1q1, and in the process changes the 0 it was initially facing to a 1, as shown in Figure 17.2. Then the Turing machine moves one step left, and in the process changes the 1 it was facing to a 0, as also shown in Figure 17.2. At this point, it enters the accepting state A, as shown by the ID of A10 attained by this Turing machine, and hence halts. The general rules below are illustrated on specific tiles mentioned by the annotation “Tn” below: