Properties Of Boolean Formulas

Properties of Boolean Formulas
Boolean satisfiability: an overview: Research on Boolean satisfiability methods (SAT) is one of the “hottest” areas in formal methods, owing to the fact that BDDs are often known to become exponentially sized. The idea of model checking without BDDs was introduced. This work also coincided with the arrival on the scene, of efficient Boolean satisfiability methods. These modern SAT solvers utilization in carrying out these algorithms. Easily modifiable versions of these tools are now freely available. Boolean SAT methods are now able to often handle extremely large system models, establish correctness properties, and provide explanations when the properties fail. Andersson presents many of the basic complexity results, including the inevitability of exponential blow up, even in the domain of SAT. We discuss a summary of these issues, and offer a glimpse at the underlying ideas behind modern SAT tools. Unfortunately, space does not permit our detailed presentation of the use of SAT techniques or some of their unusual applications in system verification. The reader may find many tutorials on the Internet or web sites.

Normal forms
We now discuss several properties of Boolean (or propositional) formulas to set the stage for discussions about the theory of NP-completeness. There are two commonly used normal forms for Boolean formulas: the conjunctive normal form (CNF) and the disjunctive normal form (DNF). Given a Boolean expression (function) over n variables x1 . . .xn, a sum-of-products (SOP) or disjunctive normal form (DNF) expression for it is one where products of literals are disjoined (OR-ed) – a literal being a variable or its negation. For example, nand(x, y) is expressed in SOP (DNF) as

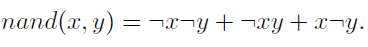
A POS (CNF) expression for nand would be (¬x ¬y). A systematic way to obtain DNF and CNF expressions from truth tables is illustrated below: basically, the DNF form for a Boolean function is obtained by disjoining (OR-ing) the min terms at which the function is a 1, while the CNF form for a Boolean function is obtained by conjoining (ANDing) the max terms at which the function is a 0. All these are illustrated in Figure 18.1.

Fig. 18.1. Min/Max terms for nand, whose DNF form is m0 m1 m2 and CNF form is M3 (the only max term where the function is 0)