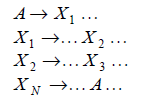Properties Of Context-free Languages

Pumping Lemma for CFG: A “Pumping Lemma” is a theorem used to show that, if certain strings belong to a language, then certain other strings must also belong to the language.

Let us discuss a Pumping Lemma for CFL.

We will show that , if L is a context-free language, then strings of L that are at least ‘m’ symbols long can be “pumped” to produce additional strings in L. The value of ‘m’ depends on the particular language.

Let L be an infinite context-free language. Then there is some positive integer ‘m’ such that, if S is a string of L of Length at least ‘m’, then

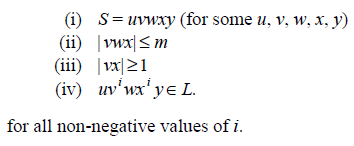
It should be understood that

1. If S is sufficiently long string, then there are two substrings, v and x, somewhere in S. There is stuff (u) before v, stuff (w) between v and x, and stuff (y), after x.
2. The stuff between v and x won’t be too long, because | vwx | can’t be larger than m.
3. Substrings v and x won’t both be empty, though either one could be.
4. If we duplicate substring v, some number (i) of times, and duplicate x the same number of times, the resultant string will also be in L.

Definitions

A variable is useful if it occurs in the derivation of some string. This requires that

(a)    the variable occurs in some sentential form (you can get to the variable if you start from S), and

(b)    a string of terminals can be derived from the sentential form (the variable is not a “dead end”).

A variable is “recursive” if it can generate a string containing itself. For example, variable A is recursive if

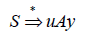
for some values of u and y.

A recursive variable A can be either

(i)  “Directly Recursive”, i.e., there is a production

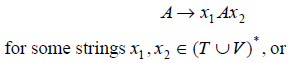
(ii)  “Indirectly Recursive”, i.e., there are variables xi and productions