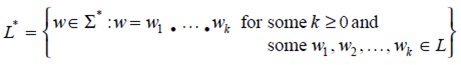Strings And Languages
The mathematical study of the “Theory of Computation” begins by understanding the Mathematics of strings of symbols.
Alphabet: It is defined as a finite set of symbols.
Example: Roman alphabet {a, b, ...... z}.
“Binary Alphabet” {0, 1} is pertinent to the theory of computation.
String: A “string” over an alphabet is a finite sequence of symbols from that alphabet, which is usually written next to one another and not separated by commas.
- If Σa = {0,1} then 001001 is a string over Sa .
- If Σb = {a, b, K, z) then axyrpqstcd is a string over Sb .
Length of String: The “length” of a string is its length as a sequence. The length of a string w is written as |w|.
Example: |10011| = 5
Empty String: The string of zero length is called the “empty string”. This is denoted by Î.
The empty string plays the role of 0 in a number system.
Reverse String: If w w w wn = 1 2K where each wi ÎS, the reverse of w is
wn wn-1 . . . w1.
Substring: z is a substring of w if z appears consecutively within w.
As an example, ‘deck’ is a substring of ‘abcdeckabcjkl’.
Concatenation: Assume a string x of length m and string y of length n, the concatenation of x and y is written xy, which is the string obtained by appending y to the end of x, as in x1, x2 Kx m y1 y2K yn .
To concatenate a string with itself many times we use the “superscript” notation:
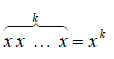
Suffix: If w = xv for some x, then v is a suffix of w.
Prefix: If w = vy for some y, then v is a prefix of w.
Lexicographic ordering: The Lexicographic ordering of strings is the same as the dictionary ordering, except that shorter strings precede longer strings.
The lexicographic ordering of all strings over the alphabet {0, 1} is (∈, 0, 1, 00, 01, 10, 11, 000, K ).
Language: Any set of strings over an alphabet Σ is called a language. The set of all strings, including the empty string over an alphabet Σ is denoted as Σ*.
Infinite languages L are denoted as
L = {w ∈ Σ* : w has property P}
Examples:
(a) L1 = {w ∈ {0,1}* :w has an equal number of 0' s and 1' s}
(b) L {w w wR}
2 = ∈ Σ * : = where wR is the reverse string of w.
Concatenation of Languages: If L1 and L2 are languages over Σ, their concatenation is L = L1 · L2, or simply L = L1L2, where
L = {w∈ Σ * :w = x · y for some x ∈ L1 , and y∈ L2}
Example: Given Σ = {0,1}
L1 {w w } = ∈ Σ * : has an even number of 0' s
L2 w w = { : starts with a 0 and the rest of the symbols are 1' s} then
L1L2 {w w } = : has an odd number of 0' s
Kleene Star: Another language operation is the “Kleene Star” of a language L, which is denoted by L*. L* is the set of all strings obtained by concatenating zero or more strings from L.