Tautology, Contradiction And Contingency

Tautology, Contradiction and Contingency

(a) Tautology: A Tautology is a propositional form whose truth value is true for all possible values of its propositional variables.

Example: pÚ ¬ p.

(b) Contradiction: A contradiction or absurdity is a propositional form which is always false.

Example:pÙ ¬ p.

(c) Contingency:A propositional form which is neither a tautology nor a contradiction is called a contingency.

Example 1: Show that P ->Q has the same truth value as ¬ P ÚQ for all truth values of P and Q, i.e., show that (P =>Q) Û (¬ P ÚQ) is atautology.

Solution:

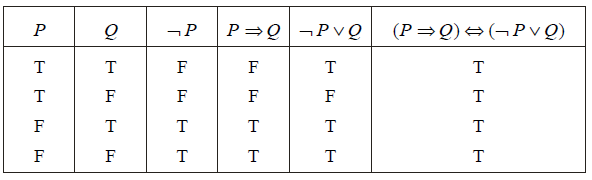
From the truth table it is clear that P =>Q has the same truth value as ¬ P Ú Q.

Also it is seen that (P =>Q) Û (¬ P Ú Q) has all truth values to be “True”. Therefore it is a “Tautology”.

Example 2: Establish whether the following propositions are tautologies, contingencies or contradictions.

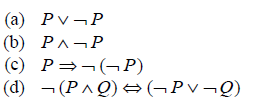
Solution: