Transition Functions For Npda
Transition Functions for NPDA: The transition function for an NPDA has the form
d : Q ´ (Σ ∪ {λ}) ´ Γ -> Finite sub sets of Q X Γ
d is now a function of three arguments.
The first two arguments are the same as before:
- the state
- either l, or a symbol from the input alphabet.
- The third argument is the symbol on top of the stack. Just as the input symbol is “consumed” when the function is applied, the stack symbol is also “consumed” (removed from the stack).
- Note that while the second argument may be l, rather than a member of the input alphabet (so that no input symbol is consumed), there is no such option for the third argument. d always consumes a symbol from the stack, no move is possible if the stack is empty.
- There may also be a l-transition, where the second argument may be l, which means that a move that does not consume an input symbol is possible. No move is possible if the stack is empty.
Example: Consider the set of transition rules of an NPDA given by
d (q1 , a, b)={(q2 , cd), (q3 , l)}
If at any time the control unit is in state q1, the input symbol read is ‘a’, and the symbol on the top of stack is ‘b’, then one of the following two cases can occur:
- The control unit tends to go into the state q2 and the string ‘cd’ replaces ‘b’ on top of the stack.
- The control unit goes into state q3 with the symbol b removed from the top of the stack.
In the deterministic case, when the function d is applied, the automaton moves to a new state q ÎQ and pushes a new string of symbols x ÎG* onto the stack. As we are dealing with non-deterministic pushdown automaton, the result of applying d is a finite set of (q, x) pairs.
Drawing NPDAs
NPDAs are not usually drawn. However, with a few minor extensions, we can draw an NPDA similar to the way we draw an NFA.
Instead of labeling an are with an element of S, we can label arcs with
a | x, y where a ÎS, x ÎG and yÎG* .
Let us consider the NPDA given by
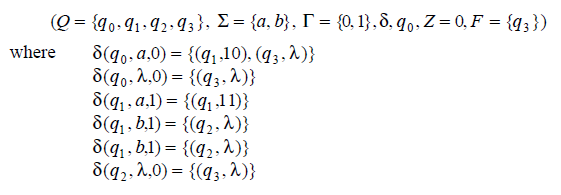
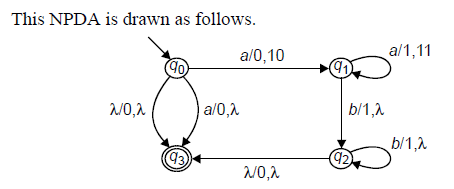
Please note that the top of the stack is considered to be the left, so that, for example, if we get an ‘a’ from the starting position, the stack changes from ‘0’ to ‘10.’.