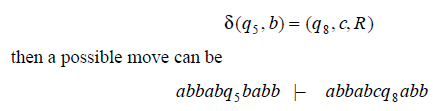Turing Machine

Turing Machine: A Turing Machine is like a Pushdown Automaton. Both have a finite-state machine as a central component, both have additional storage.

A Pushdown Automaton uses a “stack” for storage whereas a Turing Machine usea a “tape”, which is actually infinite in both the directions. The tape consists of a series of “squares”, each of which can hold a single symbol. The “tape-head”, or “read-write head”, can read a symbol from the tape, write a symbol to the tape and move one square in either direction.

There are two kinds of Turing Machine available.

1. Deterministic Turing Machine.
2. Non-deterministic Turing Machine.

We will discuss about Deterministic Machines only. A Turing Machine does not read “input”, unlike the other automata. Instead, there are usually symbols on the tape before the Turing Machine begins, the Turing Machine might read some. all, or none of these symbols. The initial tape may, if desired, be thought of as “input”.

“Acceptors” produce only a binary (accept/reject) output. “Transducers” can produce more complicated results. So far all our previous discussions were only with acceptors. A Turing Machine also accepts or rejects its input. The results left on the tape when the Turing Machine finshes can be regarded as the “output” of the computation. Therefore a Turing Machine is a “Transducer”.

Definition of Turing Machines: A Turing Machine M is a 7-tuple

(Q, S,G,d, q , # , F ) 0

where Q is a set of states

S is a finite set of symbols, “input alphabet”.

G is a finite set of symbols, “tape alphabet”.

d is the partial transition function

# ÎT is a symbol called ‘blank’

q0 Q Î is the initial state

F ÍQ is a set of final states

As the Turing machine will have to be able to find its input, and to know when it has processed all of that input, we require:

1. The tape is initially “blank” (every symbol is #) except possibly for a finite, contiguous sequence of symbols.
2. If there are initially nonblank symbols on the tape, the tape head is initially positioned on one of them.

This emphasises the fact that the “input” viz., the non-blank symbols on the tape does not contain #.

Transition Function, Instantaneous Description and Moves: The “Transition Function” for Turing Machine is given by

d :Q ´ G ->Q ´ G ´ {L, R}

When the machine is in a given state (Q) and reads a given symbol (G) from the tape, it replaces the symbol on the tape with some other symbol (G), goes to some other state (Q), and moves the tape head one square left (L) or right (R).

An “Instantaneous Description” or “Configuration” of a Turing machine requires.

(a)    the state the Turing machine is in

(b)    the contents of the tape

(c)    the position of the tape head on the tape.

This is written as a string of the form

xi. . . .  x j qmxk . . . .xl

where the x’s are the symbols on the tape, qm is the current state, and the tape head is on the square containing xk (the symbol immediately following qm).

The “Move” of a Turing machine can therefore be expressed as a pair of instantaneous descriptions, separated by a symbol “|–”.

For example, if