Two-way Finite Automata

Introduction: Two-way finite automata are machines that can read input string in either direction. This type of machines have a “read head”, which can move left or right over the input string.

Like the finite automata, the two-way finite automata also have a finite set Q of states and they can be either deterministic (2DFA) or nondeterministic (2NFA).

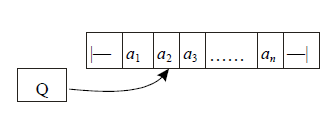
They accept only regular sets like the ordinary finite automata. Let us assume that the symbols of the input string are occupying cells of a finite tape, one symbol per cell as shown in fig. The left and right end markers |— and —| enclose the input string. The end markers are not included in the input alphabet S.

Definition

A 2DFA is an octuple

M = (Q, S, |—, —|, d, s, t, r)

where, Q is a finite set of states

S is a finite set of input alphabet.

|— is the left endmarker, |—  Ï S,

—| is the right endmarker, —|  Ï S,

d :Q ´ (S È{|—, —|})® (Q ´ {L, R}) is the tran si tion func tion.

sÎQ is the start state,

t ÎQ is the accept state, and

r ÎQ is the reject state, r ¹ t

d takes a state and a symbol as arguments and returns a new state and a direction to move the head i.e., if d ( p, b) = (q, d), then whenever the machine is in state p and scanning a tape cell containing symbol b, it moves its head one cell in the direction d and enters the state q.